経済学の基礎「効用関数」をシミュレーションで理解しよう!
目次
経済学の基礎から、シミュレーションを用いて解説していきます!
今まで本サイトでは数学の基礎部分をメインにシミュレーションで解説するコンテンツを作成してきました。
今回からはそのような知識を用いて、経済学の分野の話について解説していきます!経済学は身近なものごとに関する数の話になるので、シミュレーターを使ってイメージして理解するのが効率的だと思います!是非ご活用を!
「100万円の価値」は1万円の100倍ではない!?
まずお金とは何か、を考えていきます。ここに100万円があったとして、、、これは1万円の価値の何倍あると言えるでしょうか?
一般的には100倍の価値と言えそうですよね、、。でも、実はそれは違います。評価の仕方によりますが、100倍とは言えません。量が100倍あるからといって、価値が100倍あるとは言えないのです。
なぜならば「お金は幸せを得るための手段でしかない」からです。価値を考えるということは、それによってどれだけ幸せになれたか、満たされたかを考える必要があるんですね。
そう考えると、、、「100万円で買えるモノの満足度」が「1万円で買えるモノの満足度」の100倍あるとは言えないですよね!
「100個のリンゴの価値」は1個のリンゴの100倍にならない!
ここで分かりやすくするため、リンゴに置き換えて価値を考えていきます。つまり、「100個のリンゴの価値」が「1個のリンゴの価値」の何倍になるかを考えていきます。
この時、一般的には「100個のリンゴの価値 < 1個のリンゴの価値×100」になります。なぜなら、「モノはたくさん食べると飽きてきて無価値になってくる」からです。どんなにリンゴが好きな人でも、5個のリンゴを食べてと言われたらキツくなってきますし、嬉しくなくなってきますよね>< という感じで、基本的にモノの価値は個数が増えるたびに下がっていくんです。
食べ物だけでない。基本的にモノの価値は増えるごとに下がっていく
また、一般論ですが、食べ物だけでなく、モノの価値は量が増えるごとに下がっていきます。例えばPCやスマホ。最初の1個はすごく便利になるはずですよね。今までに出来なかったコミュニケーションが出来るようになったりとか。ただ2個目、3個目が増えてもなかなか使いこなせないですよね。幸せ度もそれによって大きくは上がるとは思えません。
また、洗濯機や冷蔵庫などの家電に関しては、面積の関係もあって、2個以上あると逆に価値が下がるということもありそうですよね><
もちろん例外もありますが、基本的にはモノが増えるたびに1個あたりの価値は下がっていくのです!

「効用関数=満足度を数値に表したグラフ」
上記のようなモノの個数と満足度の関係をうまく表すのが経済学で使用する「効用関数」です。これは横軸をモノの個数、縦軸を効用の合計値としてその関係性を表したグラフです。効用とは、上でも述べてきた満足度/幸福度/効能を数値で表した値です。「満足」という曖昧なものを、数値で表したものと考えて下さい!
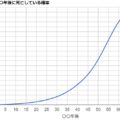
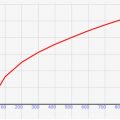
この効用関数は↓のようなグラフになります。個数が増えると、効用の合計値はもちろん増えていきます。しかし、その増え方が個数が増えるほど弱くなっていくんです。
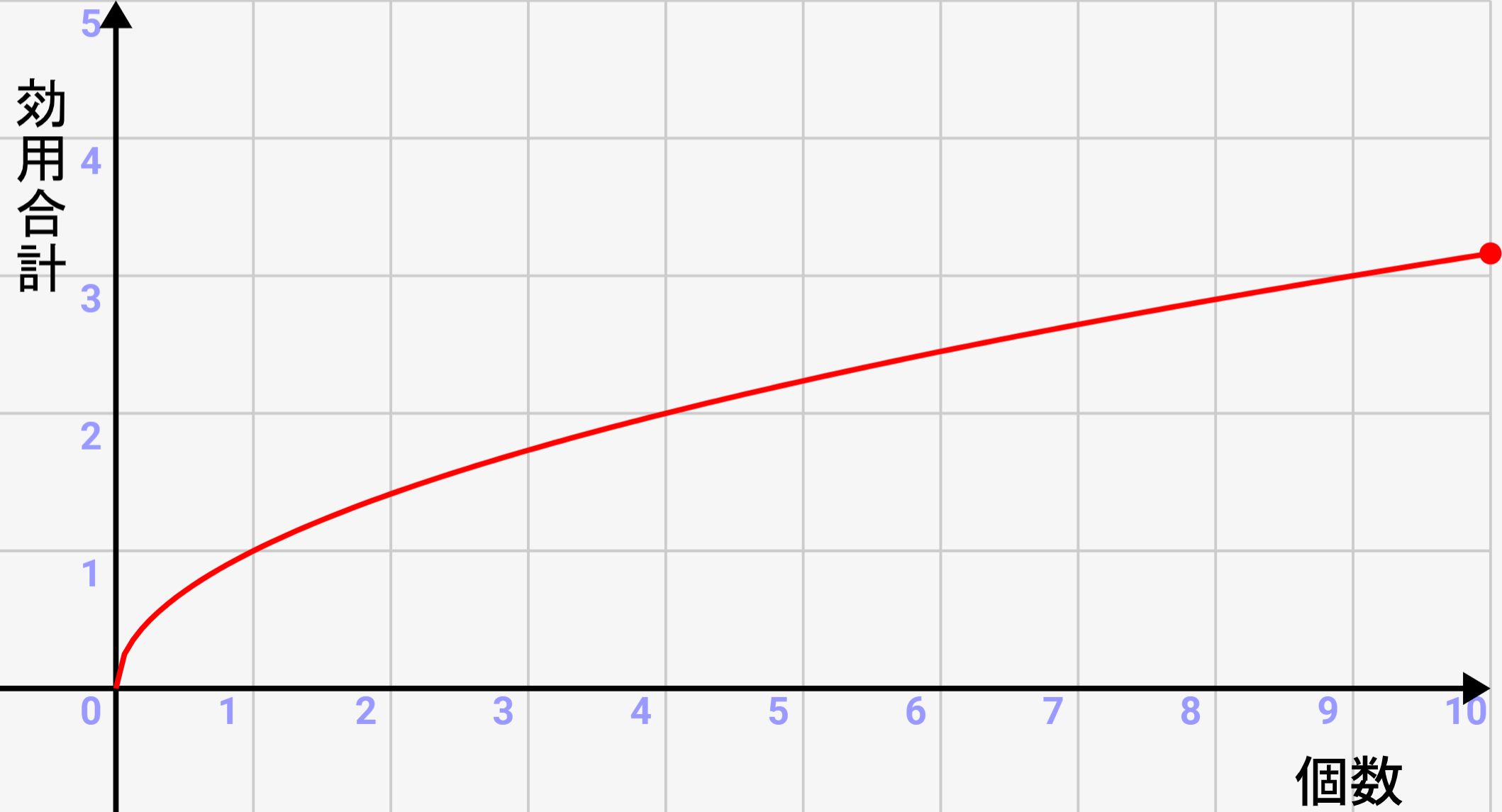
1個増えるごとにどう効用が変わるのか、詳しく解説していきます。
まず最初の1個を取得したとき、効用は↓のように青い棒の分(1目盛り分)上がります。
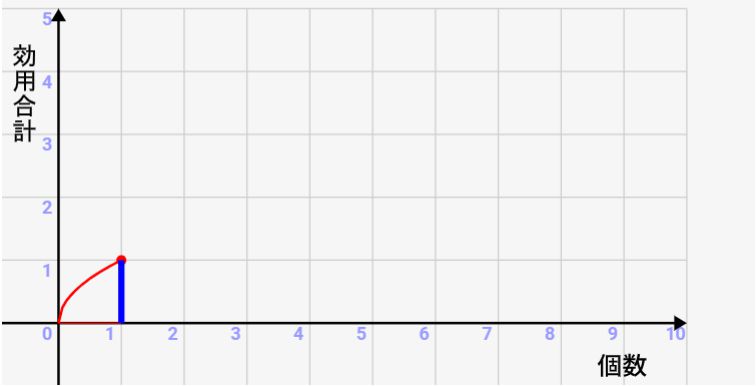
それに対して、2個目が増えた時に↓のように少ししか上がりません。上記で説明したとおり、1個目と比べて価値が下がるんです。
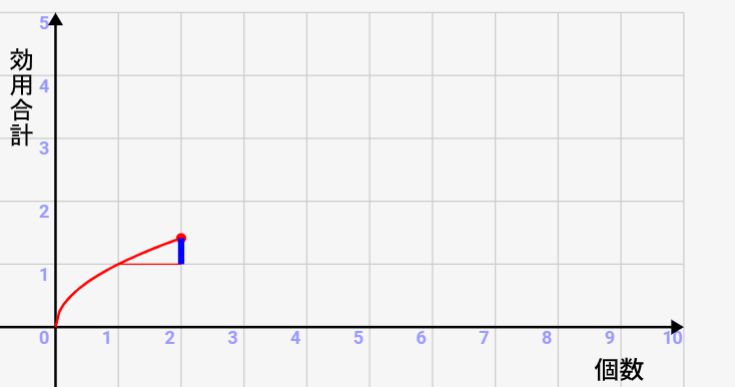
さらに3個目になると、、、もっともっと1個増えたことによる効用(満足度)は下がっていきます。
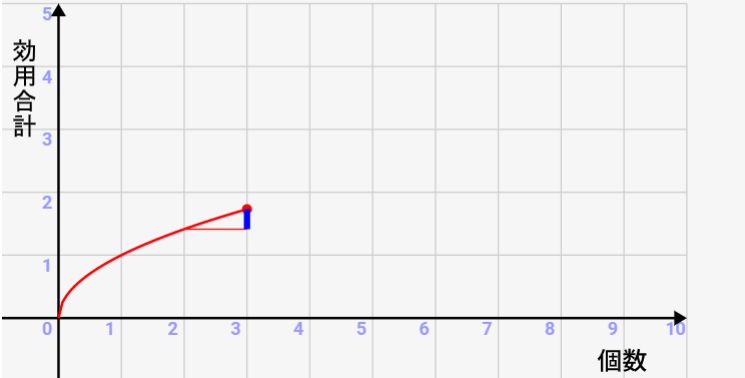
これが効用関数のグラフの特性です。グラフによって、モノの価値が下がっていくことを表している訳ですね。このように価値が少しずつ減っていくことを逓減といいます。
シミュレーションで「効用関数」のイメージをつけよう!
それでは、上記で説明した効用関数がどんなものかを、「リンゴの個数が増えていく例」で確認してみましょう!
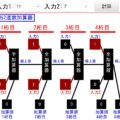
↓のシミュレーターで、灰色のリンゴをタップ/クリックすると、リンゴの数が増えていきます。そして、その個数までの効用関数グラフが表示されます。また、追加された1個のリンゴで増加した効用を青線の長さと数値で表示します。
全体効用は増えていくが、1個のリンゴの効用は減っていくことを確認しましょう!(リセットボタンを押すと、最初からカウントし直せます)
まとめ:効用関数を使うと、人間が得られる満足度をシミュレーションできる!
今回は経済学の基礎として、「効用関数」について解説しました。
上記で説明したとおり、お金の金額がそのまま効用(満足度)につながるわけではありません。特にモノの場合は飽き/必要個数等があるため、基本的には個数が増えるほど、効用が減っていきます。
もちろん、人やモノによってこの変動は変わります。しかし、この「全体の効用は増えていくけど、1個あたりの効用は減っていく」という性質は多くの場面で当てはまるはずです。
人間にはこのような満足度関数=効用関数があることを意識すると、経済活動の見方が変わってくるかもしれません><
⇒「経済学/投資」カテゴリ記事一覧
その他関連カテゴリ












はじめまして
何もわからないならがとても興味深く読み始めました。
効用関数のリンゴのシュミレ-ションがマイナスなのですが。。。リンゴ1個でマイナス1となるのはどういうわけですか?
ありがとうございます。すみません、誤りです。プラスになるよう修正しました。