コンピューターの原理基礎:足し算を行う基本論理回路をシミュレーターで理解しよう![複数桁の2進数計算/半加算器と全加算器の組み合わせ]
前回の記事で、かなり長くなりましたが、AND回路/OR回路/NOT回路でどのように2進数の1桁の計算をおこなうかを説明しました。これら3つの回路を組み合わせることにより、半加算器と全加算器という2つの加算装置が構成できます。そして、それによって1桁の2進数の足し算は実現できるのです。
でも、2進数の1桁の計算だと、1+1=2までしか計算できませんよね!それでは全く役に立ちません。そのため、本ページではこの半加算器と全加算器を使用して、もっともっと大きな数を計算できるようにしていく過程をしめしていきます。
足し算を回路で計算している流れを確認できるシミュレーターも作りましたので、是非使用してみてください!
![コンピューターの原理基礎:足し算を行う基本論理回路をシミュレーターで理解しよう![複数桁の2進数計算/半加算器と全加算器の組み合わせ]](https://retu27.com/wp-content/uploads/rapture_20170820182002-500x451.jpg)
目次
前回のおさらい:半加算器と全加算器
前回、2進数の1桁を表現する回路として半加算器と全加算器を紹介しました。この二つをもう一度軽くおさらいしておきます。
加算値=その桁の計算結果
繰り上げ値=次の桁に繰り上げとなる値
1.半加算器: 繰り上がってきた値を無視した足し算回路
半加算器は純粋に1つ目と2つ目の数の足し算をおこなう回路です。下記のように、その加算値はXOR回路という回路で、繰り上がり値はAND回路で計算可能です。XOR回路は「入力1と入力2のどちらか一方だけ1のときのみ、出力を1とする回路」です。詳しくは前回記事参照。

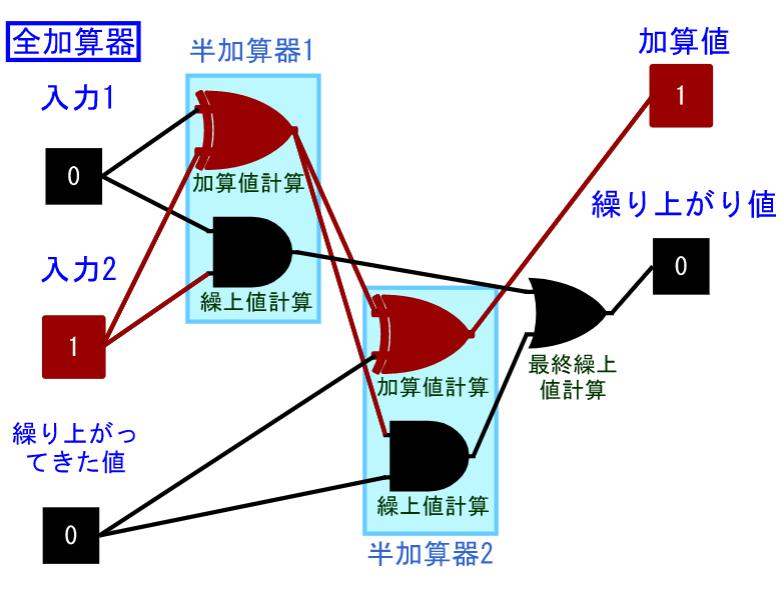
2.全加算器: 繰り上がってきた値を考慮した足し算回路
全加算器は下の位から繰り上がってきた値も考慮する回路です。入力1+入力2の足し算をしてから、その合計と繰り上がってきた値の足し算をすればいいだけなので、半加算器を2回かければいいことになります。回路は下図のとおりです。
複数桁の2進数の計算
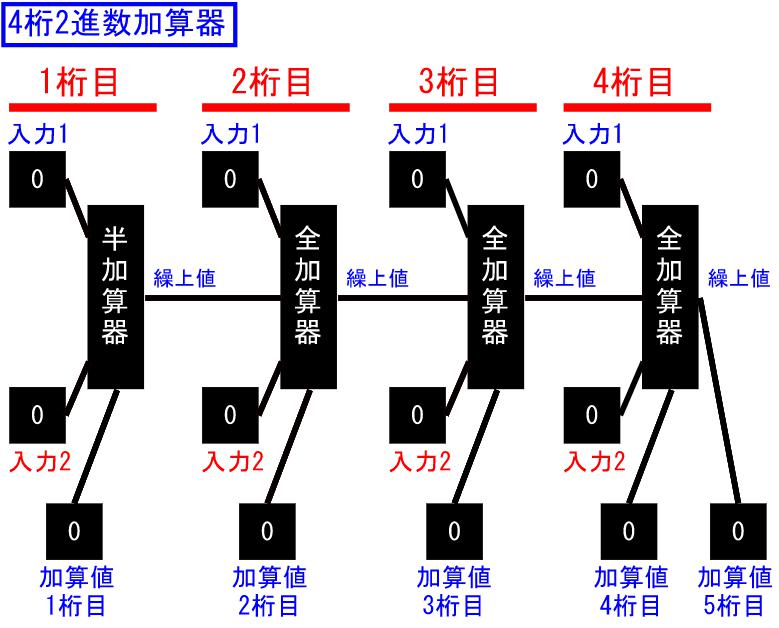
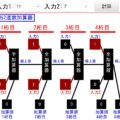
それでは複数桁の2進数を考えていきます。基本的に、半加算器と全加算器を組み合わせることで計算可能になります。簡単のために、4桁の2進数同士の足し算をする場合を考えます。そうすると、各桁は下記のような回路であらわせることが分かると思います。
2桁目:1桁目の繰り上がり値を含めて、入力1と入力2を全加算器で計算(繰り上がり発生)
3桁目:2桁目の繰り上がり値を含めて、入力1と入力2を全加算器で計算(繰り上がり発生)
4桁目:3桁目の繰り上がり値を含めて、入力1と入力2を全加算器で計算(繰り上がり発生)
5桁目:4桁目の繰り上がりの値をそのまま出力
このように、各桁は、1つ前の桁の繰り上がり値を入力として全加算器を使用することで値を計算できます。ただし、1桁目は繰り上がってくる値がないため、半加算器のみでの計算となります。また、5桁目は4桁目の計算の繰り上がり値をそのまま出力することになります(入力値がないため)。これを示したのが↓の図です。
それでは、これを実際のシミュレーターで動かしてみましょう!
2進数の足し算論理回路シミュレーター!
今までの解説を総まとめしたシミュレーターです。選択ボックスで入力値1と入力値2(10進数)を選択し、計算ボタンを押すとこの二つの足し算が始まります!
- 計算ボタンを押すと、入力値1と入力値2が2進数として評価され、各桁の入力値に代入されます(回路の関係上、左から1桁目、2桁目、3桁目、4桁目と逆順に並んでいます)
- 各桁の入力値をもとに計算が1桁目から順に開始されます
- 各半加算器/全加算器の計算では、各回路の詳細図に移動して、実際に加算器がどのように計算して加算値/繰り上げ値を計算するのかを確認することができます!
- 最終的に、全ての加算値の桁を2進数として評価した値を出力しますので、入力値1と入力値2の合計値になっていることを確認してみて下さい!
* 再度数字を変えて、計算ボタンを押すと、現在の計算はリセットされ、最初から計算がはじまります!
[参考:10進数と2進数対応表]
| 10進数 | 2進数 |
|---|---|
| 0 | 0000 |
| 1 | 0001 |
| 2 | 0010 |
| 3 | 0011 |
| 4 | 0100 |
| 5 | 0101 |
| 6 | 0110 |
| 7 | 0111 |
| 8 | 1000 |
| 9 | 1001 |
| 10 | 1010 |
| 11 | 1011 |
| 12 | 1100 |
| 13 | 1101 |
| 14 | 1110 |
| 15 | 1111 |
まとめ:単純な回路を組み合わせるだけで、ものすごく難しいことができるようになる!
それでは、最後にまとめです。
このコンピューターの原理基礎の記事では、最初の基本的な論理回路(AND回路/OR回路/NOT回路)の役割をまず説明しました。
そして、それらを組み合わせて1桁の2進数計算ができる半加算器と全加算器の構成の仕方をこちらのページで解説しました。
最後にこのページで、それら半加算器と全加算器を組み合わせることで、足し算を瞬時に行える回路が作れてしまうことを示しました。
このように、単純な回路から、人間でも瞬時にはできないような計算回路が構築できてしまうのです!
今後もCPUなどの仕組みを解説し、なぜ機械は複雑なことが可能なのかを順を追って解説していきたいと思います!乞うご期待です!
- 一桁目に半加算器、二桁目以降に全加算器を置くと複数桁の加算器が完成する
- 加算器は1桁目から順に計算していき、順に繰り上がって演算していく
- このような回路の組み合わせでコンピューターは高速に四則演算可能になっている
⇒「CPU」カテゴリ記事一覧
その他関連カテゴリ









わかりやすい