年収が増えても幸福度はそこまで上がらない!?「年収と効用関数の関係」をシミュレーションで理解しよう!
目次
経済学の基礎から、シミュレーションを用いて解説していきます!
今まで本サイトでは数学の基礎部分をメインにシミュレーションで解説するコンテンツを作成してきました。
今回からはそのような知識を用いて、経済学の分野の話について解説していきます!経済学は身近なものごとに関する数の話になるので、シミュレーターを使ってイメージして理解するのが効率的だと思います!是非ご活用を!
前回のおさらい:効用関数=満足度を数値に表したグラフ
まずは前回説明した効用関数についておさらいしておきます。
一般的にモノの量が多くなってくると、1個あたりの価値/満足度が下がってきます。例えば食べ物。1個目は美味しいと思ったとしても、10個目には飽きているはずですよね。また、家電などでも1,2個までは嬉しくてもそれ以上になるともはや無意味になるものも多いですよね。一般的にモノの価値は数が増えるごとに下がっていきます。
この、モノの個数と満足度の関係をうまく表したのが経済学で使用する「効用関数」です。これは横軸をモノの個数、縦軸を効用の合計値としてその関係性を表したグラフです。効用とは、上でも述べてきた満足度/幸福度/効能を数値で表した値です。「満足」という曖昧なものを、数値で表したものです。
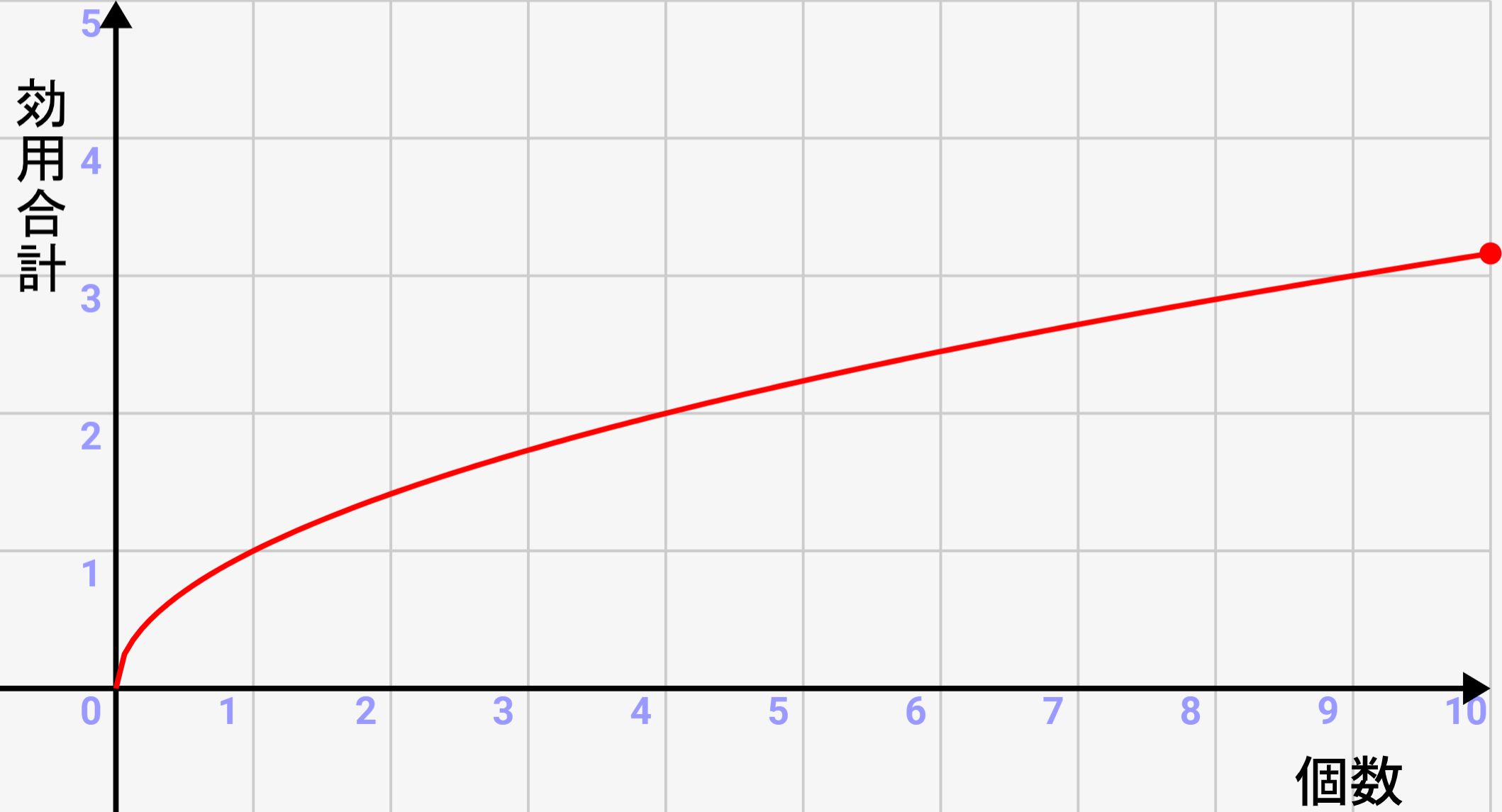
この効用関数は↓のようなグラフになります。個数が増えると、価値は増えますが、個数が増えるほど価値が薄れていきます。
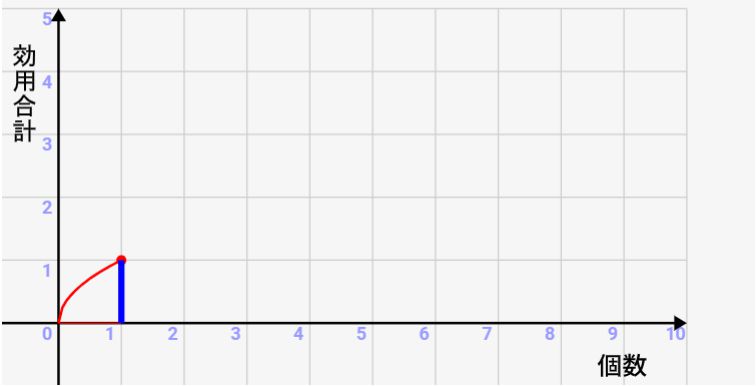
まず最初の1個を取得したとき、効用は↓のように青い棒の分(1目盛り分)上がりますが、、、
2個目が増えた時に↓のように少ししか上がりません。数が増えるたびに増加効用は下がっていきます。
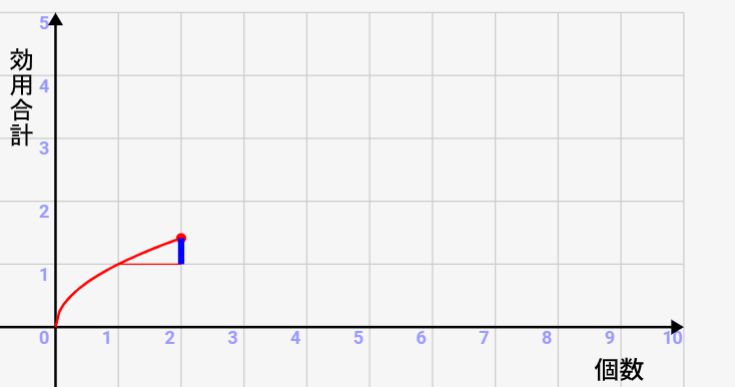
1つモノが増えたことによる効用の増加量を限界効用と呼びます。また、その限界効用が薄れていくことを「限界効用逓減の法則」と呼びます。
年収が上がると効用はどのように上がる?年収と効用関数の関係!
モノの個数が上がると、上記のように効用は上昇していきますが、その価値上昇度は緩やかになっていきます。では、年収があがると、効用はどのように変わるのでしょうか。
基本的にはモノの価値と同等に、緩やかに増加していくことになります。年収が上がると、使えるお金も増えますが、買えるものの種類に限りがあるため、結局は効用関数と同じような曲線を描くことになるからです。
これを考察するためには、「各年収で最大限に効用を上げるモノの購入方法」を考える必要があります。これは、
年収100万円で効用を最大に上げるモノの購入パターン
年収200万円で効用を最大に上げるモノの購入パターン
…
と各年収で最大に効用(満足度)を上げるモノの購入数を計算して、各年収での最大値をグラフとして線でむす結ぶことで求まります。
そうすると↓のようなグラフになります。なかなかイメージしにくいので、簡単なシミュレーションで実験してみましょう!
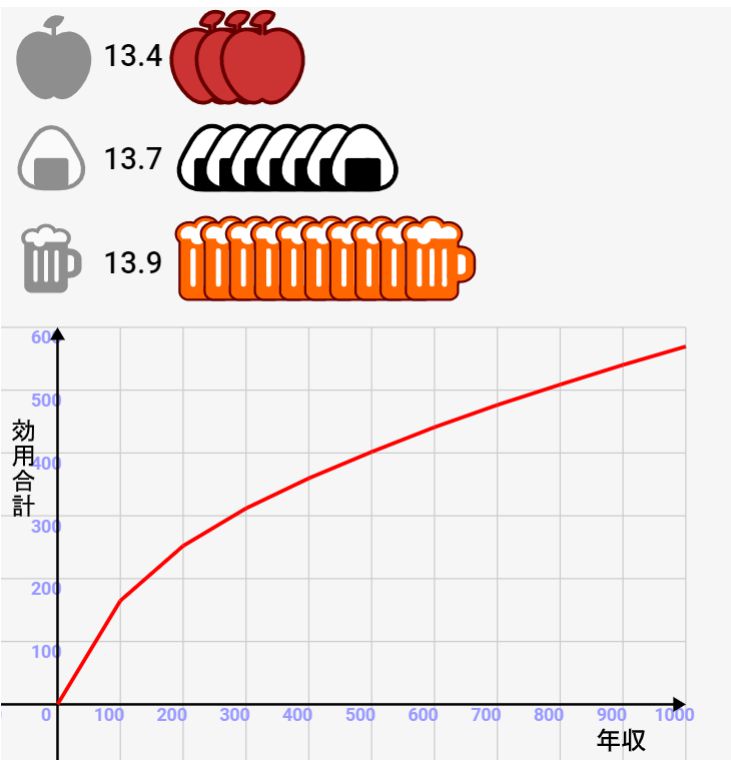
年収と効用の関係性をシミュレーターでグラフ化してみよう!
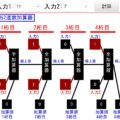
このシミュレーターでは各年収の地点で、灰色のリンゴ/おにぎり/ビールのどれかをクリックすると購入できます。簡単のためにどれも1個50万円としてます。簡易的な実験のため現実的な金額じゃないのはご了承下さいませ>< 本当はモノの種類がもっと多くて、もっと小刻みにモノは購入されるはずですが、動きとしては同様になるはずです。
リンゴ/おにぎり/ビールの効用は以下の関数で表せると仮定します。ビールが一番効用が大きくなっています。ただ、それぞれの購入個数によって限界効用の上下関係は変わってきます。例えばビールを購入しすぎると、リンゴよりも価値が薄れてくるんですね。
\( おにぎりの効用 = 75* \sqrt{個数} \)
\( ビールの効用 = 75* \sqrt{個数} \)
各地点で残金が0円になるまでモノを購入し、「+100万」ボタンを押して年収を増やしていきましょう。それを繰り返すと、各年収と得られる効用の関係をグラフで描くことが出来ます!
リンゴ/おにぎり/ビールの横の数字は、次にそのモノを購入したら得られる効用を示しています。基本的には、この数字が最も大きいものを購入すると、最大の効用が得られるはずです!
現合計効用:0
シミュレーション結果考察
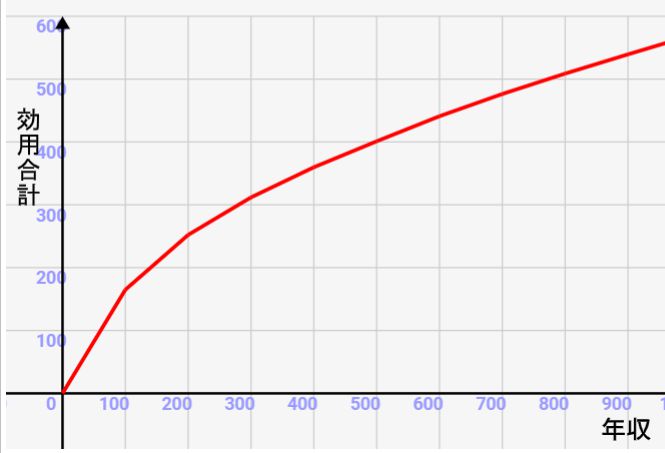
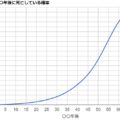
各年収地点で、最大の効用が得られるパターンを選ぶと↓のような購入パターンとグラフになるはずです!
ビールの効用を一番高くしているので、最適な購入パターンではビールの購入数が最大になりますね。ただ、効用が比較的低いリンゴも購入することになることがキーポイントですね。各モノの効用は購入するたびに、どんどん下がっていくので、このように色んなモノを購入するのが最適パターンになるんですね。
また、基本的には、モノの効用関数と同じく、逓減するようなグラフになるのがわかります。つまり、年収が上がると、効用(幸福度)は上がっていくけど、その差はどんどん小さくなっていくわけですね!
例えば上のグラフでは500万円の時点で効用400を超えていますが、1000万円の時点では550程度しか効用がありません。単純に年収が2倍になるからって、効用が2倍にはならないんですね。実際そんなにお金あっても購入するものも限られてきますし。
今回はあくまでシミュレーター上の実験ですが、結構現実にもこれに近い幸福度になるのではないでしょうか。ソースにもよりますが、年収600万で幸福度は頭打ちになるとよく言われたりもします(詳細はコチラの外部記事参照)。
人の幸せに関する部分なので、人によって意見異なることもあるかと思います。しかし、単純に稼いだお金に比例して幸せになるわけではないってことは多く同意が得られる事実なのではないでしょうか><
⇒「経済学/投資」カテゴリ記事一覧
その他関連カテゴリ










面白くわかりやすいです