「複素数の極形式」とは何かをシミュレーターで理解しよう![数学入門]
このページでは複素数について、分かりやすく解説しています!
今回はまず「複素数の極形式とは何か?」をシミュレーターを用いて分かりやすく説明します!
![「複素数の極形式」とは何かをシミュレーターで理解しよう![数学入門]](https://retu27.com/wp-content/uploads/20220305225355-500x498.png)
おさらい:虚数、複素数とは
虚数とは
虚数とは↓のような仮想な数のことです。
虚数iの定義
虚数i = 二回かけると-1になる仮想的な数
i*i = -1
\( i = \sqrt{-1} \)
また、コチラのページで解説したとおり、「虚数iをかける=90度回転させる」という意味を持ちます。
複素数とは
実数+虚数の組み合わせを一つにしたものを複素数といいます。
複素数の定義
複素数 = 実数と虚数の組み合わせ
例えば「+1.9 + 2.9i」という形です。
複素数は↓のように二次元のグラフで表現します。これを複素数平面といいます。
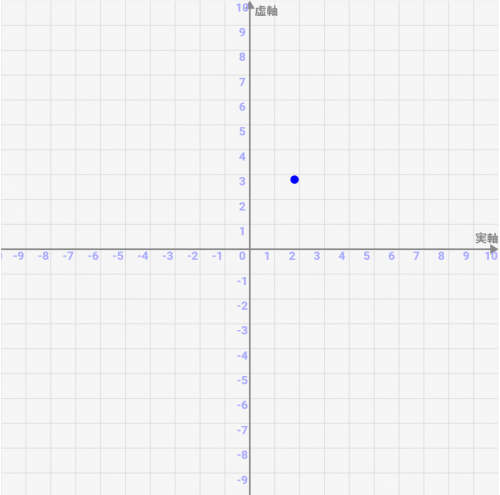
複素数のもう一つの表し方:極形式
複素数は前回記事の例のように「+1.9 + 2.9i」という形で示しました。
しかし、その他にも複素数を表すための方法があるんです。それが極形式になります!
極形式の定義
複素数を↓のように長さrと偏角(角度)θであらわしたもの
複素数z = \(r(cosθ + i \ sinθ)\)
コチラのページでも解説していますが、三角関数cosとsinを使えば、↑のように半径rと角度θで位置を表せるんですね。
また、複素数の場合はこの角度を偏角といいます!
例えばr=7,θ=30°だった場合は↓のようになります。
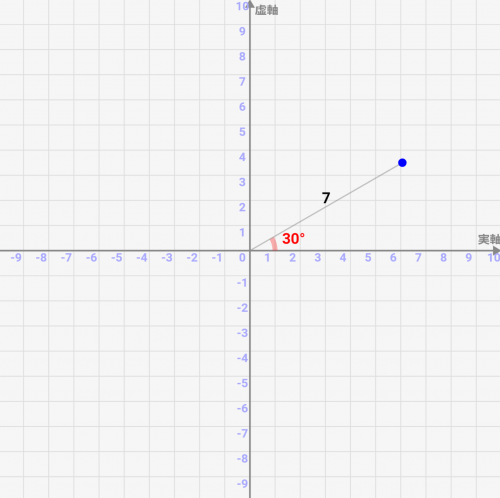
角度θと半径の長さrさえ決まれば、点の位置が一つに決まるので、このような極形式での表し方が可能なんですね!
「複素数の極形式」をシミュレーターで理解しよう!
それでは解説してきた、「複素数の極形式」をシミュレーターで確認してみましょう!
シミュレーターの説明
- ↓で極形式の長さrと偏角θをそれぞれ指定できます
- 指定した極形式の複素数が、複素数平面でどこに示されるかを確認しましょう
- 指定された極形式複素数を、通常形式でも↓で表示します
[表示複素数]
「複素数の極形式」まとめ
- \(r(cosθ + i \ sinθ)\)という形で複素数を表すことを極形式という
- 極形式でも複素数は一意に表すことができるので、標準形の代わりに用いることができる
[関連記事] コンピューターでの小数の表し方
⇒「複素数」カテゴリ記事一覧
その他関連カテゴリ















