「コンデンサーの原理」をシミュレーションで理解しよう![物理入門]
前回の記事で「無限に広がる平板」における一様電界について解説しました。今回はその考え方を発展させて「コンデンサの原理」について解説します!
![「コンデンサーの原理」をシミュレーションで理解しよう![物理入門]](https://retu27.com/wp-content/uploads/20211124007077-500x464.png)
一様電界のおさらい
点電荷の場合は\( 4πkq\)と電荷qに比例した力線が出ましたが、一様電界の場合は1㎡あたりの電荷密度δに比例した力線数がでていきます。
総計で、力線数は↓となります。
力線総数 = \( 4πkδ \)
- k : 比例係数。真空中で\(9.0 × 10^9\)
- δ : 電荷密度[\(C/m^2\)]
ここで、電場の強さEを考えると、力線は上下面で半分ずつ出ていくはずのため、↓のようになります。力線の半分が実際に構成さされる電場Eになるわけです。
E = \( N/2 \) = \( 2πkδ \)
↓のように平板の両側にE=\( 2πkδ \)の電界が発生するイメージです。

「コンデンサ」は両側に反対の電荷を持つ平板を持つ!
上記の通り、一様電界では平板一枚で発生する電界を考えましたが、コンデンサでは↓のように電荷Qを持つ平板(青色)と電荷-Qを持つ平板(赤色)の2つがペアになる場合を考えます。
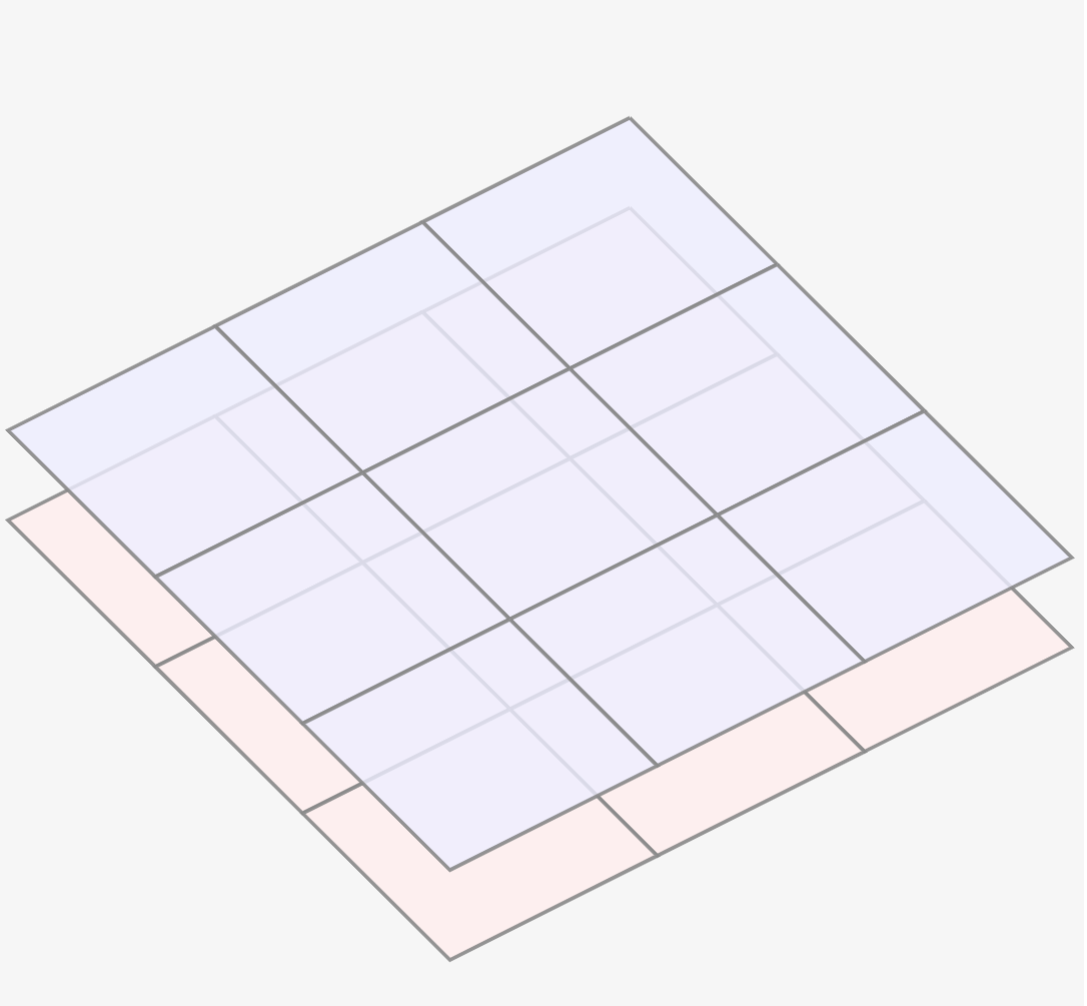
この場合、青色のプラスの電荷では板から離れる方向に、赤色のマイナス電界は引き寄せる方向に電界が発生します。この2つはQ,-Qと真逆の電荷を持つので、電界も真逆です。
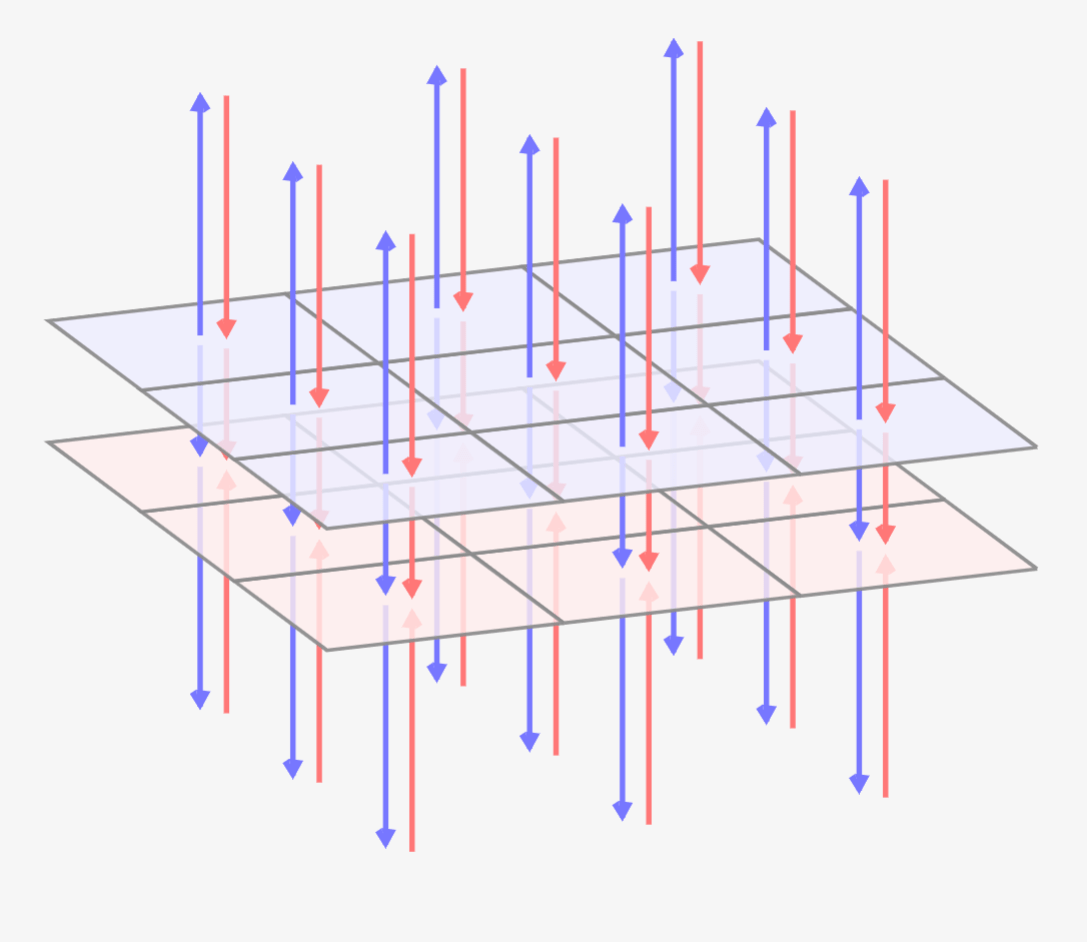
このときに、総合的に生み出される電界は「青と赤の2つの電界を足し合わせた電界」です。その電界は↓のようになります。
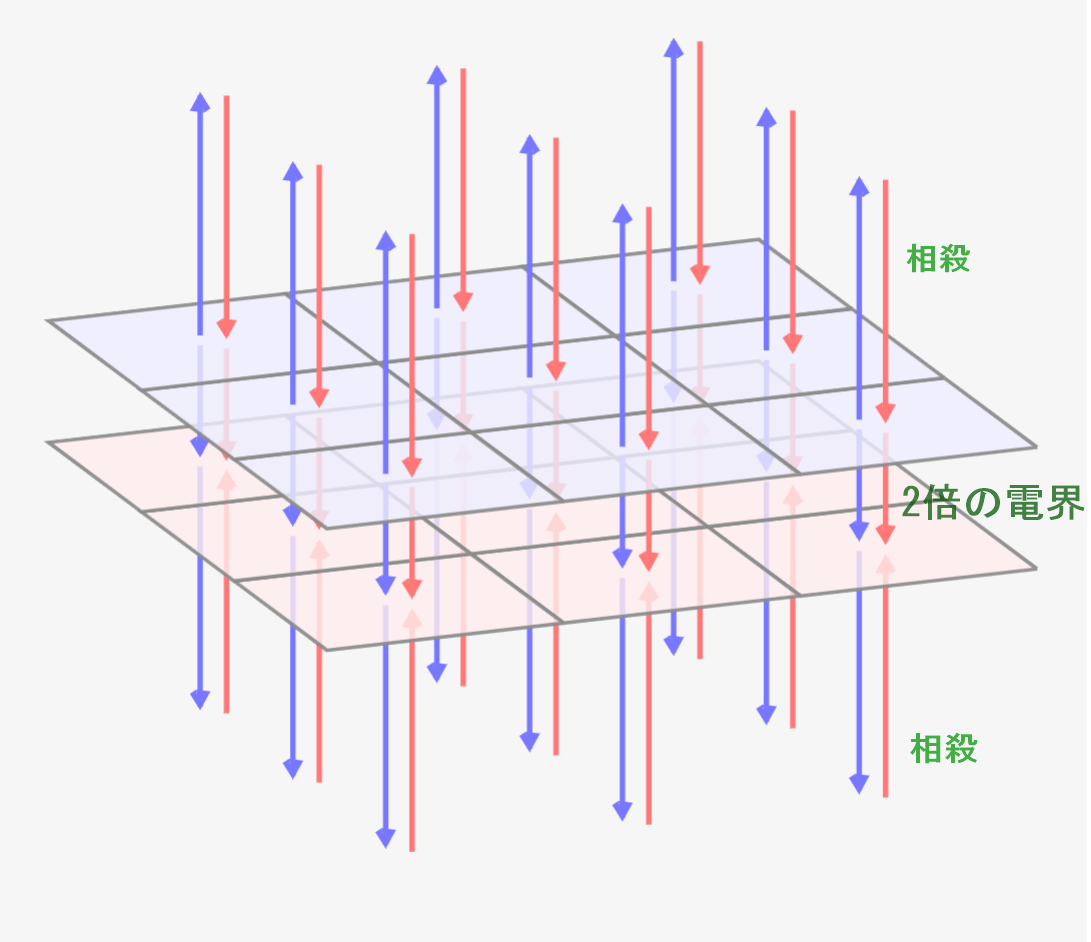
逆方向の電界は相殺しあいます。二枚の平板の上と下の部分を見ると、矢印が反対でペアになっていますね。なので相殺し合うのです。
逆に、平板の間は電界の向きが両方とも下向きになっています。足し合わせなので、電界の強さは2倍になるんです!
故に、二枚の平板の間の電界の強さは↓のようになります。
E = \( (コンデンサがつくる電界)*2 \) = \( 2πkδ * 2 \)
= \( 4πkδ \)
- k : 比例係数。真空中で\(9.0 × 10^9\)
- δ : 電荷密度[\(C/m^2\)]
電荷が平板に全体でQ,-Qだけあり、平板の面積がSだとすると、電荷密度\(\large{δ=\frac{Q}{S}}\)となるため、↓のように変形できます。
\(E = 4πkδ \) = \( \displaystyle \frac{4πkQ}{S} \)
- k : 比例係数。真空中で\(9.0 × 10^9\)
- Q : 電荷量[\(C\)]
- S : 平板面積[\(m^2\)]
ここで電位を考えると、「V=Ed」なので、コンデンサが作る電位Vは↓のようになります!
\(V = \displaystyle \frac{4πkQd}{S} \)
- k : 比例係数。真空中で\(9.0 × 10^9\)
- Q : 電荷量[\(C\)]
- d : 平板間距離[m]
- S : 平板面積[\(m^2\)]
「コンデンサーの原理」をシミュレーターで確認しよう!
それでは「コンデンサ」を3次元のシミュレーションで実際に見て確認しましょう!
- スライドバーによって電荷密度δ,平板間距離dが変えられます
- 青色矢印がプラス電荷の平板による電界、赤色矢印がマイナス電荷の平板による電界を示しています
- 分かりやすいように、電気力線本数=電荷密度×2となるように図示しています。つまり2πk=1という過程をおいています
- 区画1つが1㎡を示しています。今回はS=9㎡です。
- 電荷の量によって電気力線が比例して増えることを確認しましょう
- 上下の電界が相殺され、結局平板間の電界だけ残ることを確認しましょう
- 下の表示角度で見やすいように縦角度を変えて確認できます
- 平板間の距離dに比例して、電位Vが大きくなることを確認しましょう
↓表示角度(上下)をコチラのバーで調整可能です!
2つの平板により、上下の電界が相殺され、最終的に平板間だけに2倍の電界ができます。また、その距離に比例して電位Vが増加します。シミュレーターを用いてこの重要なポイントを理解しておきましょう!
- 平板電荷を2枚重ねると、うまく相殺し合い、板の間だけに電界Eが発生する
- 電位V=dEのため、平板間の距離dに比例した電位Vが構成される
⇒「静電気・電場」カテゴリ記事一覧
その他関連カテゴリ
















