「一様電界」をシミュレーションで理解しよう![物理入門]
前回の記事で、点電荷におけるガウスの法則について解説しました。今回はそれとは別の「一様電荷」について考えてみます
![「一様電界」をシミュレーションで理解しよう![物理入門]](https://retu27.com/wp-content/uploads/20211028006980-500x460.jpg)
目次
ガウスの法則のおさらい
最初に前回記事のおさらいです。ガウスの法則は、点電荷からでる電場・力線の総数を数えると、実は距離に関わらず一定という法則でした。
半径r球の力線総数 = \( \large E × 4πr^2 \)
= \(\large \displaystyle \frac{4πr^2 kq}{r^{2}} \) = \( \displaystyle \large 4πkq\)
- k : 比例係数。真空中で\(9.0 × 10^9\)
- q : 電荷の電気量[C]
↓イメージにするとこんな感じですね。中心から固定の線がでてくるイメージです。これなら、距離が離れても、球面上を通る線の総数はどこでも一定になるのです。

「一様電界」は無限に広がる平面板を想定した電界!
さて、今回考えるのでは点電荷のように「中心から広がる電界」でなく、平面からでる電界です。
この電界を考える場合は「無限に広がる平面板」を想定します。↓のような二次元の面が無限に広がっていて、そこに電荷が偏ることなく分布してるようなイメージです。

一様電界の場合、電界は球面の場合と違い、↓のようになります。板と垂直に進んでいく感じです。重要なのは、片側だけでなく、「裏表両側に電界が伸びていく」ということです。図でいうと、上と下両方向から電界がでていく感じです。

一様電界でも考え方は同じ
一様電界の力線の数も、点電荷の場合と考え方は同じです。点電荷の場合は\( 4πkq\)と電荷qに比例しましたが、一様電界の場合は1㎡あたりの電荷密度δに比例した力線数がでていきます。
総計で、力線数は↓となります。
力線総数 = \( 4πkδ \)
- k : 比例係数。真空中で\(9.0 × 10^9\)
- δ : 電荷密度[\(C/m^2\)]
ここで、電場の強さEを考えると、力線は上下面で半分ずつ出ていくはずのため、↓のようになります。力線の半分が実際に構成さされる電場Eになるわけです。
E = \( N/2 \) = \( 2πkδ \)
「一様電界」をシミュレーターで確認しよう!
それでは「一様電界」を3次元のシミュレーションで実際に見て確認しましょう!
- スライドバーによって電荷密度が変えられます
- 分かりやすいように、電気力線本数=電荷密度×2となるように図示しています(片面に電荷密度 本の電界がつくられる)
- 区画1つが1㎡を示しています(本当はこの区画が無限に広がっていますが、今回は9区画のみ表示)
- 電荷の量によって電気力線が比例して増えることを確認しましょう
- 上下同じ数の力線が出て、均等に電場Eが構成されることを確認しましょう
- 下の表示角度で見やすいように縦角度を変えられます
- 電荷の符号が逆になると、矢印が逆になることを確認しましょう
↓表示角度(上下)をコチラのバーで調整可能です!
シミュレーション結果の要点
力線・電場は電荷密度に比例する
↑のシミュレーター結果でわかるように、電気力線と電場Eは電荷密度δに比例して多くなります。
電荷密度=1.0の場合1区画に1つの力線が描かれます

電荷密度=4.0の場合1区画に4つの力線が描かれます

電場の向きは電荷の符号によってかわる
電荷がプラスならば↑のように、矢印が出ていく方向になります。しかし、マイナスの場合は矢印が無限平面に向かって入ってくるような形になります。全く逆方向の矢印になるんです!
マイナスの場合は矢印の向きがかわる

電場・電界の強さはどこでも一定!!
これが最重要の事実です。
点電荷の場合、↓のように中心から離れるほど電気力線の密度が低くなり、電場・電界の強さが落ちていきました。
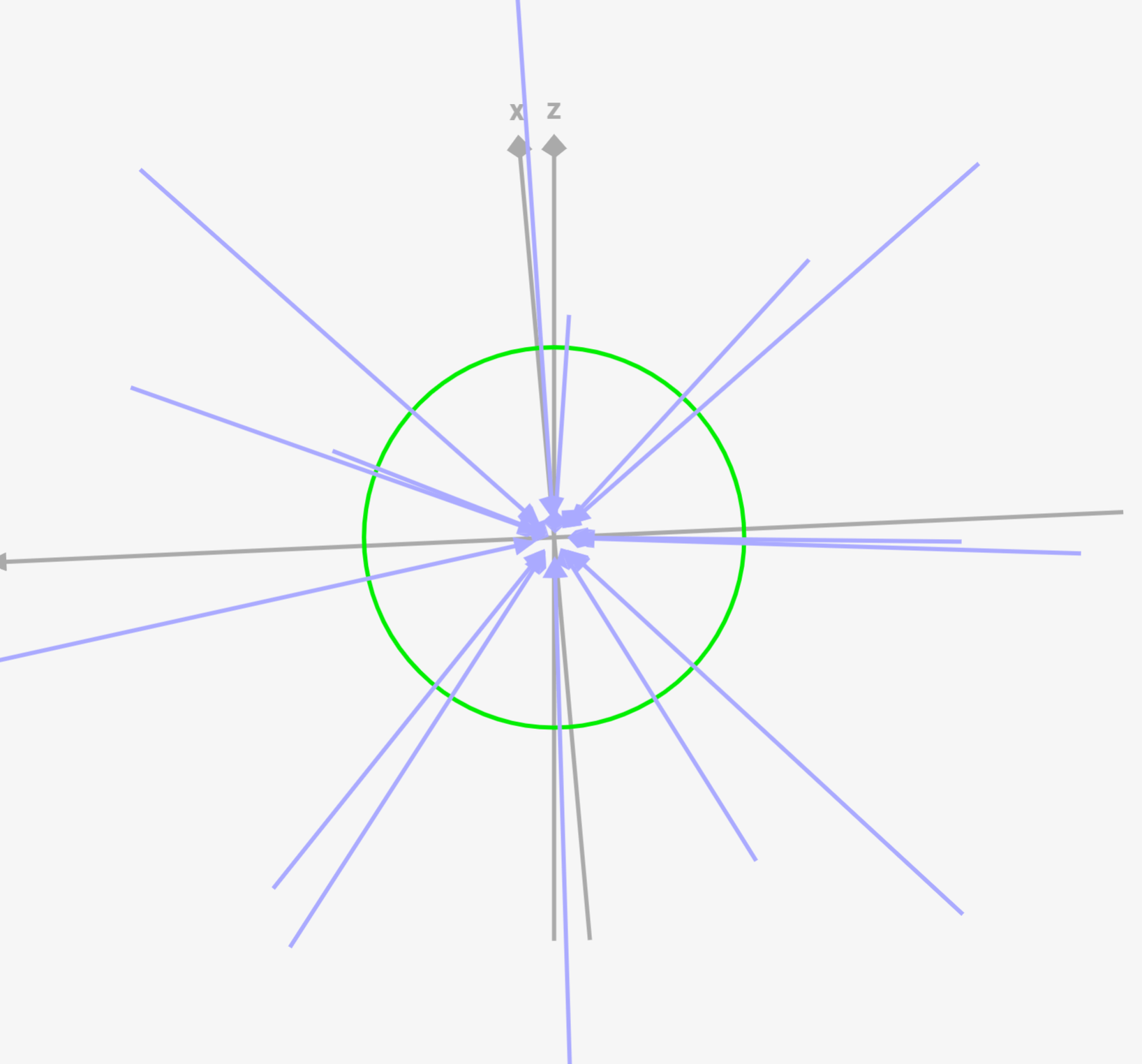
しかし、一様電界の場合、常に電気力線は平面板と垂直に伸びていくため、どこでも同じ密度になります。故に、電場・電界の強さはどこでも一定で E = \( 2πkδ \)となるんです!

- 点電荷の場合は360度に電気力線が出ていくが、一様電界の場合は板に垂直に電気力線が出ていく
- 一様電界の場合、板との距離によらずに E = \( 2πkδ \)の電界が発生する
- 電荷によって出ていく電気力線の密度が異なってくる
⇒「静電気・電場」カテゴリ記事一覧
その他関連カテゴリ
















