物理入門:「合力・力の合成(2次元・3次元) 」をシミュレーターを用いて理解しよう!
前回の記事で、合力という考え方について説明しました。しかし、前回は簡単に合力を1次元の力の組み合わせで考えました。
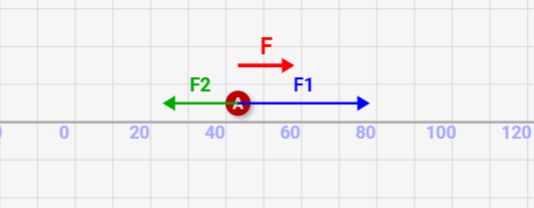
↓のように2つの力がかかった場合、その足し算である赤矢印が、最終的なかかる力となり、加速度につながるんです。
今回は2次元と3次元で合力・力の合成についてシミュレーターを用いて考えていきます!
目次
2次元・3次元でも力の合成は足し算!
それでは、2次元・3次元の力の合成について考えていきます。といっても、基本は1次元と同じです。2次元でも3次元でも全ての力を足すだけです。
2次元・3次元の力を足す時には通常の数字では表現できません。本サイトの数学記事で解説していますが、ベクトルで表現するんです。
ベクトルとは、2次元なら(x,y)、3次元なら(x,y,z)という形で方向を表現する方式です。
例えば↓のように二次元ベクトルを表せます。
これは絵にすると↓のとおりです。x=3,y=2なのでこのような矢印が引けるわけです!

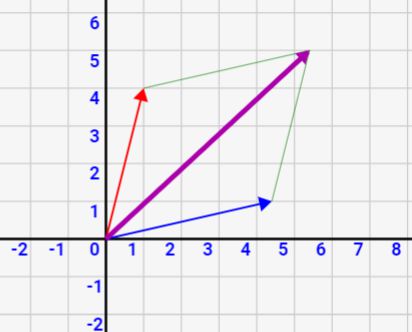
このようなベクトルで表すと、ベクトルの足し算で合力が計算できます。絵にすると↓のような感じで、赤矢印と青矢印を平行四辺形のように合成した紫矢印が合力となります。

シミュレーターで「合力(2次元)」の意味を理解しよう!
それでは上記の「合力・力の合成」をまずは2次元で確認してみましょう!
- スライドバーで赤矢印と青矢印のベクトルを変化できます
- 。各々の矢印を変えると、合力である紫矢印の方向がどう変わるか観察してみましょう
- ベクトルは数式表記でも表示されるので、合力が各ベクトルの足し算になっていることを確認してみましょう。
色々値を変えて確認しましょう!
\(\vec{a}\)成分(赤矢印)
\(\vec{b}\)成分(青矢印)
シミュレーターで「合力(3次元)」の意味を理解しよう!
次に3次元のパターンです。2次元と同様に各力(ベクトル)を変更できるので、合力がどのように変化するか観察してみましょう!
- スライドバーで赤矢印と青矢印のベクトルを変化できます
- 。各々の矢印を変えると、合力である紫矢印の方向がどう変わるか観察してみましょう
- ベクトルは数式表記でも表示されるので、合力が各ベクトルの足し算になっていることを確認してみましょう。
値を変えて確認してみましょう!
\(\vec{a}\)成分(赤矢印)
\(\vec{b}\)成分(青矢印)
「合力・力の合成(2次元・3次元) 」に関する重要なポイント
上のシミュレーターで理解しておくべき重大なポイントは、「2次元でも3次元でも、合力は両方のベクトルを平行四辺形のように足し合わせた矢印となる」ということです。
↓は3次元の場合ですが、青矢印と赤矢印を足し、平行四辺形のように足し合わせた形で紫色の合力が出来上がっています。

この平行四辺形こそ、合力のイメージです。このイメージを頭にいれておきましょう!
- 2次元/3次元の場合は、ベクトル的に力を足せば合力が求まる
- 合力は、元の力ベクトルを平行四辺形のように足し合わせた形になる
⇒「力の基本原理」カテゴリ記事一覧
その他関連カテゴリ














