物理入門:「力の分解(2次元・3次元) 」をシミュレーターを用いて理解しよう!
前回の記事で、2次元・3次元での合力の計算方法を解説しました。
今回はその反対の、「力の分解」についてのお話です。ある斜め力が働いているとき、そのままでは計算しにくかったりします。そこで、力の合成とは逆に、力を2ベクトルに分解することで計算しやすくしたりします。
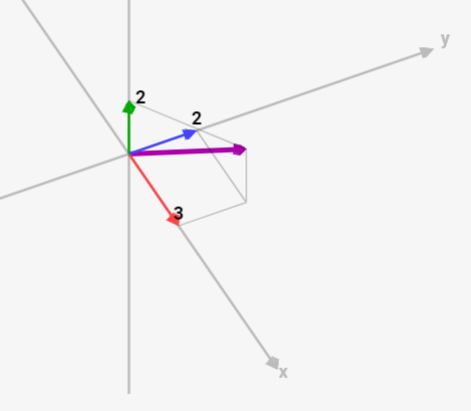
力は任意の2つのベクトルに分解できる!
前回は合成ベクトル・合力の計算の仕方を説明しました。ベクトル的に加算するんですね。
今回説明する「力の分解」は、その逆。「2つ加算すると、対象の力と一致するような2つの力(ベクトル)に分解する」という操作です。
例えば、↓は力の分解の例です。元の力は紫のものですが、青と赤の力に分解することができます。なぜなら、青と赤を足し合わせると、元の紫の力になるからです。このように、元の力を2つの力に分解できるんです!
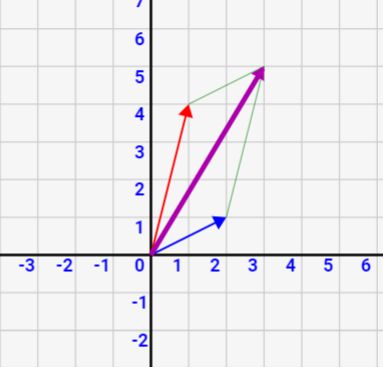
分解のパターンは無限大にある
注意としては、力の分解の仕方は無限にあるということです。↓は上と同じ合力を違う形で分解したものです。この青と赤を足しても同じ合力となります。
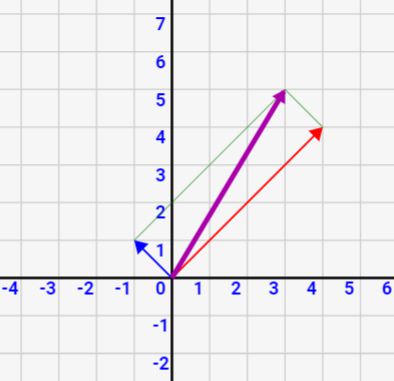
足して合力に一致すればいいので、分解方法は無限にあるんです。上記の合力ベクトルは\(\vec{a}=(3,5)\) なので、例えば↓のように、無限にベクトルを分解出来るわけです!
(1,1)と(2,4)
(1,2)と(2,3)
(-1,3)と(4,2)
よく使う標準形の成分分解方式
上記のように力の分解のパターンは無限にありますが、その中でもよく使うのはx,yと各成分ごとに分解する方式です。
3次元:(x,y,z) → (x,0,0)と(0,y,0)と(0,0,z)
絵で描くと2次元の場合は↓のような形ですね。
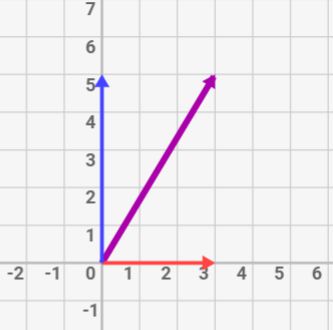
3次元の場合は↓のように3つの成分に分解します。

このように各矢印(力)が垂直になるように分解するのが標準形です。
「合力(2次元)」シミュレーター!
それでは上記の「力の分解」の意味を、シミュレーターを使って確認してみましょう!
まずは2次元からです。
- スライドバーで合力の成分を指定できます
- その合力は紫で表示され、標準形で力を分解したベクトル(力)が赤と青で表示されます
様々な力ベクトルを作ってみて、力の分解のイメージを掴みましょう!
「合力(3次元)」シミュレーター!
次は3次元の力の分解です。3次元の場合は3つのベクトルに分解するのが基本です。
- スライドバーで合力の成分を指定できます
- その合力は紫で表示され、標準形で力を分解したベクトル(力)が赤と青で表示されます
合力ベクトルの値を変えて、分解される様子を確認しましょう
- 1つの力は、複数の力に分解できる
- 分けた力をベクトル的に足し合わせたら、元の力と同一になればOK
⇒「力の基本原理」カテゴリ記事一覧
その他関連カテゴリ














