「ベクトルとはなにか?」をシミュレーション/図解で理解しよう![数学入門]
本ページでは数学のベクトルの基礎について、シミュレーターを用いてその意味・定義について解説しています。
今回は「ベクトル」とは何かについて、基礎から詳しく説明していきます!二次元ベクトルと三次元ベクトル両方のシミュレーター用意してますので、ベクトルのイメージが必ず掴めるかと思います!
![「ベクトルとはなにか?」をシミュレーション/図解で理解しよう![数学入門]](https://retu27.com/wp-content/uploads/rapture_20210228151209-477x500.jpg)
目次
ベクトルは「向き」と「大きさ」を持つ矢印のこと!
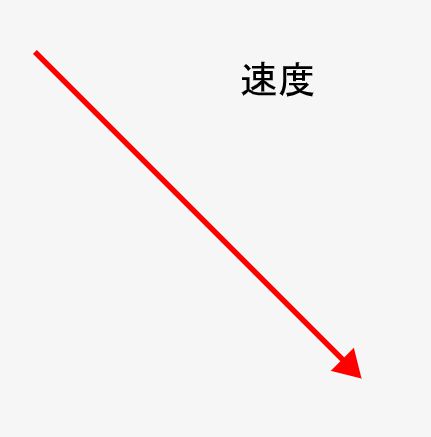
物理の世界ではただの1つの数値では表せない事象が沢山あります。その典型例が「速度」です。速度は時速30km/hというように数値でも表現できますが、それだけでは「どちらの向きに移動しているか」が分かりません。
そこで、ベクトルでは↓の図のような矢印でその「大きさ」と「向き」を表現します。矢印の方向で「向き」を、その長さで「大きさ」を表現します。
これなら、どれぐらいの速度でどちらの方向に移動しようとしてるか明白になります!↓の右下に30kmで移動していることが分かります。
その他のベクトルの例
「速度」の例以外にも、ベクトルを使う場面は沢山あります。
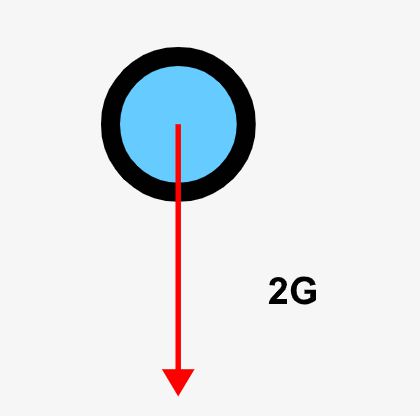
力ベクトル
物理では力をベクトルで表します。「どちらの方向に力がかかっているか」が重要になるからです。重力を例に上げると、↓のように下向きに力がかかっていることをベクトルで表現することができます!
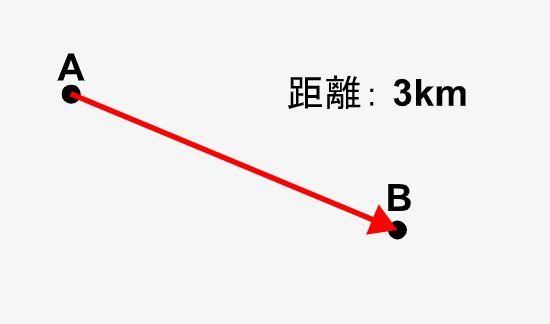
距離ベクトル
これは地図上で重要になってくるベクトルです。A地点とB地点、3km離れていると言われてもどっち向きに離れているか分かりません。そこで↓のようにベクトルを用いると、3kmという距離と同時にその方角が正確に表せます。
ベクトルの様々な表し方
ベクトルは↓のような記号で表します。上に矢印付きの線があったら、ベクトルであることを表しています。
\( ベクトルa \)
\( \displaystyle = \vec{a} \)
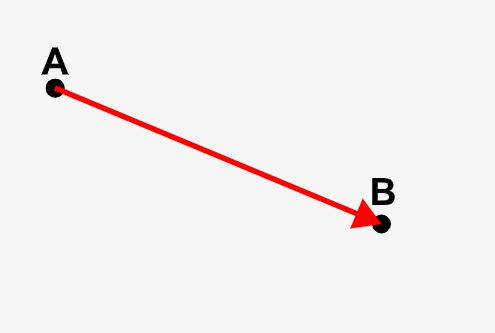
その他にも、↓の図のように始点と終点が決まっているとき、ベクトルの始点と終点の文字を使って表現することもあります。これだとドコからドコに向かうベクトルなのか明白ですね。
\( AからBに向かうベクトル \)
\( \displaystyle = \vec{AB} \)
ベクトルは複数の成分で表現できる!
ベクトルの方向をどのように数値で表すかというと、、、↓のように複数の数値を組み合わせて表現します。
例えば2次元上では、x軸方向の数値と、y軸方向の数値を使って以下のようにベクトルを表します。
\( ベクトルa \)
\( \displaystyle = (x,y) \)
ベクトルをxとyの2つの数値で表現するわけですね。このベクトルを表現するx,yを成分と呼びます。
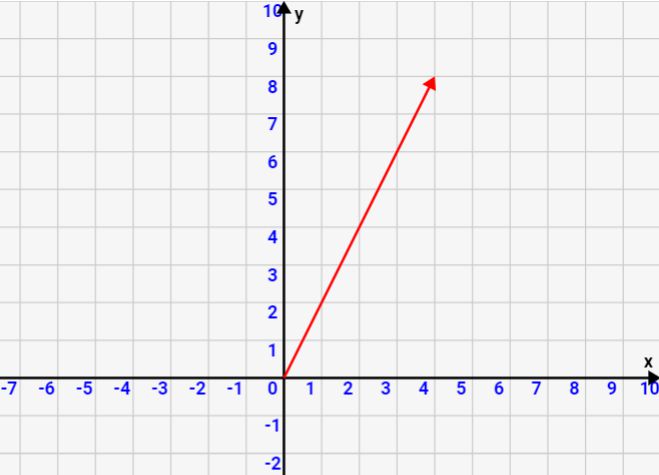
ここで例を1つ挙げます。ベクトル\(\vec{a}\)=(4,8)は↓のように表現できます。x軸(横)に4、y軸方向(縦軸)に8進んだ方向を表すベクトルになります。
また、3次元では↓のようにベクトル成分表現します。x,yに加えてzで高さを表現して3次元空間の方向を表すわけですね!
\( ベクトルa \)
\( \displaystyle = (x,y,z) \)
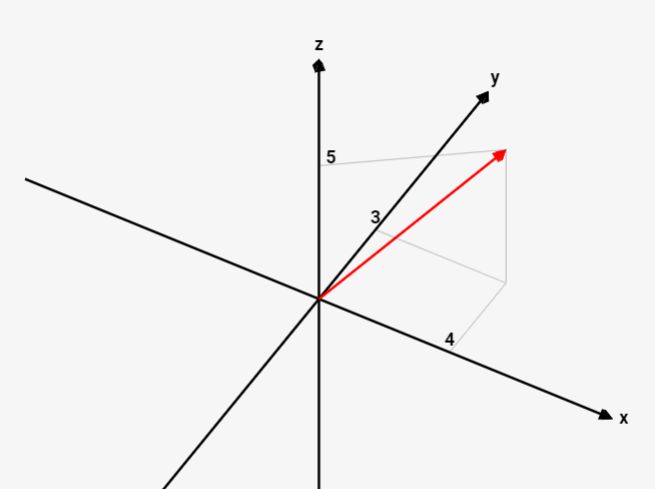
↓は\(\vec{a}\)=(4,3,5)の例です。x,y軸(平面)に加えて、高さz軸が加わって3次元空間の方向を指し示しています。
ベクトルをシミュレーターで描いてみて理解を深めよう!
上記のようにベクトルでは複数の成分を用いて、その方向を表現します。実際にシミュレーターで各成分を変えてみて、どのようにその方向が変わるか確かめてみましょう!
2次元ベクトル シミュレーター
まずは簡単に2次元の例からです!
- x,y成分を変更すると、赤矢印のベクトルが動きます
色々変更してみて実験してみて下さい!
3次元ベクトル シミュレーター
次に3次元の例です!
- x,y,z成分を変更すると、赤矢印のベクトルが3D空間の中で動きます
- 見やすいように常に回転しているので、様々な角度からベクトルを観察しましょう
3つの成分を組み合わせれば、3次元のどんな方向でも示せることを確認しましょう!
「ベクトル」まとめ:ベクトルは方向を表現するもの!様々な場面で使われます!
最後にまとめです。ベクトルは上記のように方向を表すために出てきた概念です。ベクトルを用いると、「大きさ」だけでなく、複数の成分を使って「方向」を指し示せます。方向が重要となる速度や距離、力など様々な場面で使われます。物理の世界では必須の概念ですので、上記のシミュレーターでイメージを掴んでおくと良いと思います!
次回はベクトルの「大きさ」について解説していきます!
- 数値と違って、ベクトルには方向がある
- 力や距離など方向を表す必要があるものにはベクトルを使う
- ベクトルはx,y,zなど複数の座標を使って表す
⇒「ベクトル」カテゴリ記事一覧
その他関連カテゴリ