微分シミュレーター：二次関数の微分！関数とその導関数(微分)の関係をアニメーションで確認可！
2020-05-04 
高校で習う微分、公式は習うのですが、実際にどういった関数グラフになっているかとか、元の関数との関係性が分かりにくかったりしますよね＞＜
微分(導関数)は「元の関数の各点での接線の傾き」を表したものです。ですので、元の関数の接線を描き、その傾きをグラフ化すれば微分(導関数)になっているんです！その関係性がわかるような、シミュレーターを実際に作ってみました！パラメタを変えると、どういった関数/導関数(微分)のグラフになるかをシミュレーターがすぐにアニメーション化してくれます！
微分(導関数)の求め方/考え方については、コチラの記事で詳しく説明していますので、まずはそちらをご参照願います。
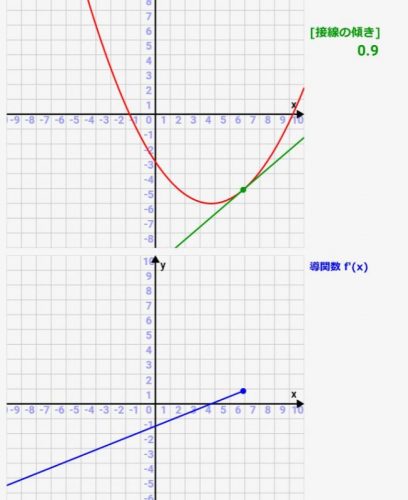
微分シミュレーター：二次関数
このシミュレーターでは関数
\( y= { ax^2 + bx + c } \)
の各パラメタa~cを変更すると、関数グラフがそれに従って描かれます。また、各点の接線とその傾きを調査しながら、導関数(微分)グラフを描いていきます！
[関数]
\( {y=} \) + 1\( {x^2 } \) + 1\( {x } \) + 1
\( {y=} \) + 1\( {x^2 } \) + 1\( {x } \) + 1
[微分(導関数)]
\( {y=} \) + 1\( {x } \) + 1
\( {y=} \) + 1\( {x } \) + 1
↓値を変えて、二次関数を変更してみて下さい
↑動的に再生速度を変えられます。左端で0にすると、一時停止となります。
二次関数の導関数(微分)の要点
二次関数は上記の通り、微分すると一次関数、つまり直線になります。つまり接線の傾きでみると、「傾きが一定速度で上がっていく/下がっていく」のが二次関数になるわけです。
↓コチラのように二次関数の極大値/極小値の時、導関数(微分)はy=0でx軸を通ります！つまり、導関数f'(x)=0の点を探せば極大値/極小値が分かるわけです。
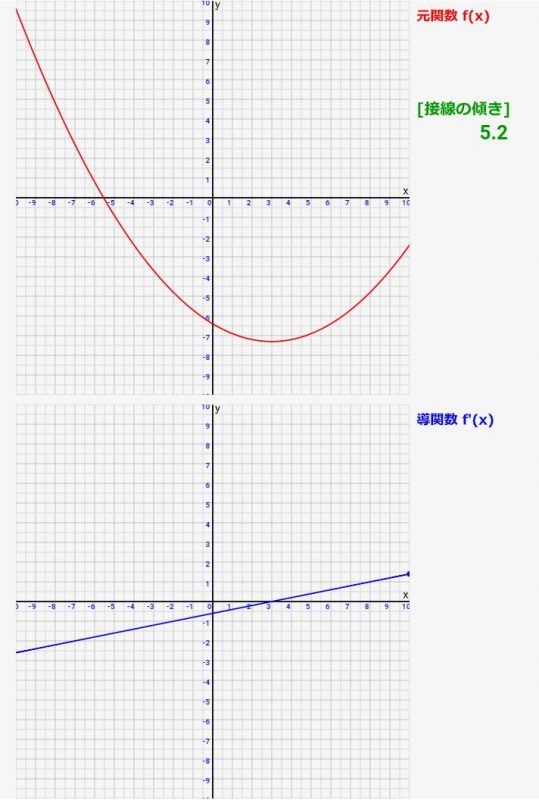
「二次関数の微分」まとめ
- 二次関数の微分は直線(一次関数)となる
↓本記事のような微分シミュレーターを各関数で用意しています。色んな関数で実際の「関数」と「導関数(微分)」の関係を確認してみて下さい！
[関連記事] 微分シミュレーション
2．二次関数の微分(本記事)
⇒「微分シミュレーター」カテゴリ記事一覧
その他関連カテゴリ