「市場の自動余剰最適化」をシミュレーターで理解しよう!自由競争市場では自然に利益最大化される![経済学入門]
今回は「市場の自動余剰最適化」についてお話しします。前回、社会的余剰の定義について話ましたが、今回はその余剰がどのように自然に自動最適化されていくかをお話します!
目次
社会的余剰とは?(復習)
各種余剰定義の復習
まず、消費者と生産者の総余剰についてですが↓のように定義できます。各者が支払い/販売できる許容額をもっていて、それと実際の価格の差異が余剰になるわけですね。
絵にすると↓のような感じです。各者の許容額との価格との差異の合計ですので、毛極赤い部分の面積が総余剰になります。
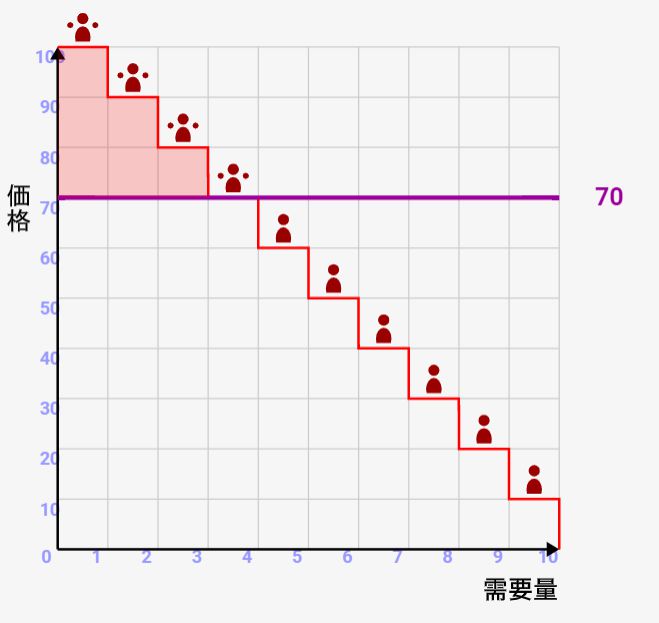
コレに対して、社会的余剰は、↓のように定義できます。
つまり、社会的余剰は消費者余剰と生産者余剰の全ての総和になります。
絵にすると↓のようになります。赤色部分が消費者余剰で、青色が生産者余剰です。この合計が社会的余剰になります。
価格ラインと需要グラフ/供給グラフとで示される面積が、総余剰となる
上の画像では、消費者/生産者が一人ひとり見えるぐらいの少量での取引を表すグラフでしたが、量が多くなっていくと、階段状の凸凹がなくなっていき、この許容額を描いた線は需要/供給グラフになっていきます。
各生産者の許容額(原価)を描いたグラフ → 供給グラフ
つまり、消費者余剰は↓のように需要グラフと価格ラインの間の面積で表すことができ、
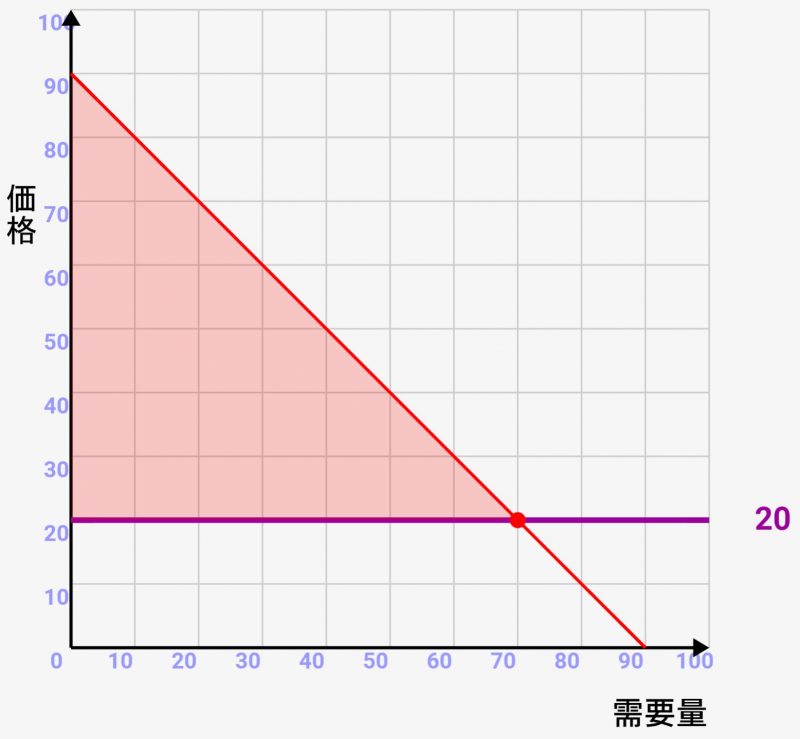
生産者余剰は、供給グラフと価格ラインの間の面積で表すことができるわけです。
↓総生産者余剰は、供給グラフと価格ラインの間の面積に比例

自然競争市場では価格は需要グラフと供給グラフ交点に収束していく → 社会的余剰が最大化される!
説明していきた社会的余剰ですが、自然競争市場では勝手に最大化されるという性質をもっています。誰かが操作しなくても、全体最適になっていくんですね!
それはなぜかを軽く説明します!
社会的余剰は、需要グラフと供給グラフの交点で最大化される
前回の記事でも説明しましたが、社会的余剰は「需要グラフ」と「供給グラフ」の交点で最大化されます。↓のグラフの絵のとおりですね。

そもそも、消費者余剰と生産者余剰の定義を考えるとわかりますが、各余剰は↑の色付き三角形の領域内でしか発生しません。取引量は需要量と供給量の小さい方の値になるためです。そうなると、自動的に全領域を余剰にできる↑の状態が最大値といえるわけです。
市場は自動的に需要グラフと供給グラフの交点に均衡していく
これはコチラの記事で解説したお話ですね。自然競争市場では、どんな初期価格であっても、↓のようにパターンごとで力が働くので、自動的に需要グラフと供給グラフの交点に価格が収束していきます。
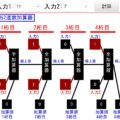
パターン1:「 供給量 > 需要量」の場合 → 価格は下がる
パターン2:「 供給量 < 需要量」の場合 → 価格は上がる
パターン3:「 供給量 = 需要量」の場合 → 価格はそこで安定
シミュレーターを使って社会的余剰が自然と最大化されることを確かめよう!
上記の社会低余剰の自動最適化の過程をシミュレーターで確認しましょう!
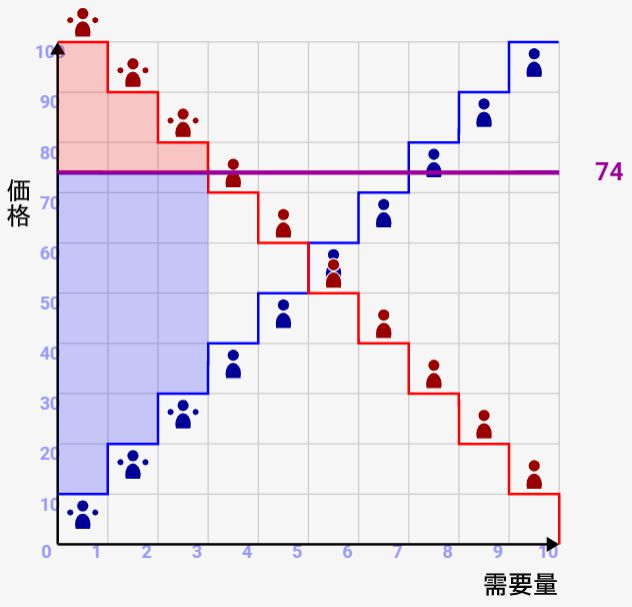
上記の説明と同じく、赤背景部が消費者余剰、青背景部が生産者余剰となっています。また、取引可能となった人は、↓のように手を上げるポーズで示しています。生産者と消費者の取引数が同一でないといけないので、同数が手を上げているはずです。
![]()
シミュレーター1: 需要/供給グラフは固定の場合
まずは価格が固定している場合でシミュレーターで実験してみましょう!
- 価格(紫線)を変動させて、実験してみましょう
- 初期価格をどこにしても、最終的には需要/供給グラフの交点に収束していきます
- 価格が収束すると、総余剰である社会的余剰が最大化されていることを確認しましょう
- 価格調整中は勝手にバーが動いてしまうので、その間に動かしてみて下さい!
色々値を変えて実験してみましょう!
総消費者余剰= 0
総生産者余剰= 0
シミュレーター2: 需要/供給グラフも変動する場合
次は↓のバーで需要/供給グラフを変更できる場合を考えてみましょう。これは、市場で需要と供給の状況が変わった場合の想定です。需要/供給のバランスがかわると、余剰が最適になる価格も変わります。しかし、自然競争市場では、そのような変化があると勝手に余剰最適化してくれるんです!
- バーで需要/供給グラフを変更できます
- 価格(紫線)以外にも、需要/供給の量を変え、ちゃんと価格が最適化されていくか確認してみましょう
- 価格調整中は勝手にバーが動いてしまうので、その間に動かしてみて下さい!
色々値を変えて実験してみましょう!
総消費者余剰= 0
総生産者余剰= 0
まとめ:自然競争市場では、勝手に消費者/生産者の総余剰(利益)が最適化される!
シミュレーターで動かして見るとわかりますが、どんな初期価格でも自然と余剰最大化となる最適価格に収束していきます。また、需要と供給の状況が変わっても、自然と余剰が最大化するように収束していきます。誰かが手を入れなくても、勝手に社会全体の利益が最大化するようになっているんですね!
↓需要/供給グラフを移動しても、自動的に余剰最適化されていく
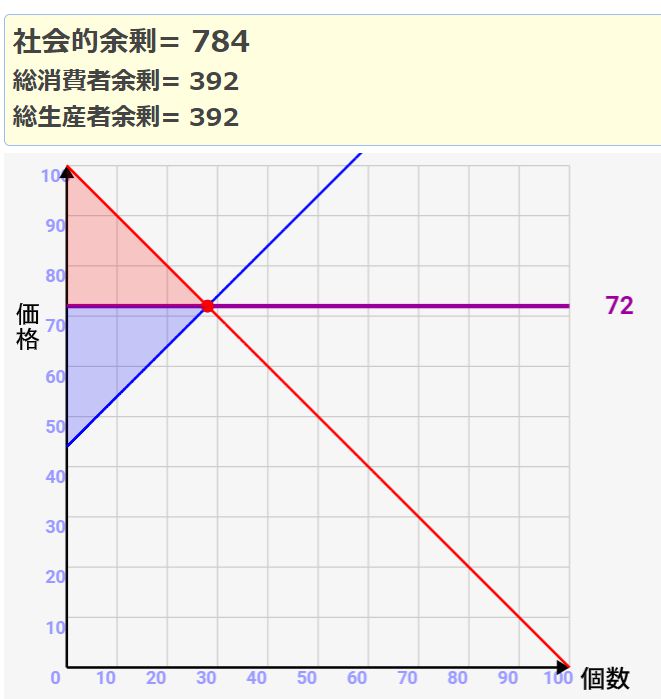
各者が利己的に動いても、勝手に社会的に最適化されるんですね。ただし、これは理想的な自由競争市場の話です。ここに独占企業が入ってきたり、輸出入が入ってきたり、色んな要素が入ってくると、社会的余剰が成り立たなくなってきます。
また、消費者余剰と生産者余剰の配分が最適になるとも限りません。今回は平等になるような需要/供給グラフの傾きでしたが、状況によっては消費者が一方的に損をするような状況になってしまいます。
そこで、「国家が最適に働くように介入していく必要がある」という話になっていくのですが、、、。それはまた別記事で少しずつ説明していきますね!
- 社会的余剰は需要と供給が一致する点で最大化される
- 需要が過多だと値段は上がり、供給が過多だと値段は下がるため、自然と需要と供給は均衡点に向かう
- その結果、自然と社会的余剰は最大化される
⇒「経済学/投資」カテゴリ記事一覧
その他関連カテゴリ