「社会的余剰」をシミュレーターで理解しよう！[経済学入門]

2021-02-23　 経済学/投資

今回は「社会的余剰」についてお話しします。社会的余剰は消費者余剰と生産者余剰の総和です。この社会的余剰の決まり方について理解していきましょう！

社会的余剰とは？

社会的余剰の定義

今回説明する社会的余剰ですが、↓のように定義出来ます。

つまり、社会的余剰とは、ただ単純に総消費者余剰 と 総生産者余剰を足しただけです。そして、この足し合わせたものが、市場の効率性を表す指標になります。

効率的で良い市場とは「社会的余剰＝総消費者余剰と総生産者余剰の総和を最大化する市場」と定義出来るわけです！

総消費者余剰と総生産者余剰は単純に足し合わせできない

前回の記事でシミュレーターで学習した「総消費者余剰」「総生産者余剰」を単純に足し合わせるだけでは正しくありません。

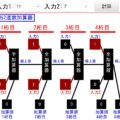
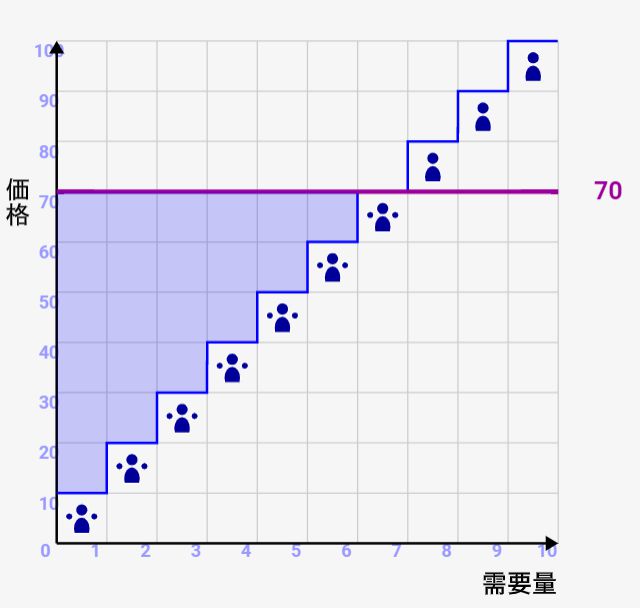
例えば価格ライン70円で各余剰は↓のようになりますが、、、

↓総消費者余剰＝60

↓総生産者余剰=210

決して、社会的余剰は合計の270にはなりません。なぜなら、「取引数は、消費者と生産者で同一でなければいけない」からです。消費者の取引数が4なら、生産者も取引数4にならないといけないんです。

ですので、↑の例では、取引数は数の少ない消費者の数に限定されます。ですので、取引数＝4です。

ですので、生産者余剰は↓で緑枠で示している領域(4人)の合計である180に限定されます。

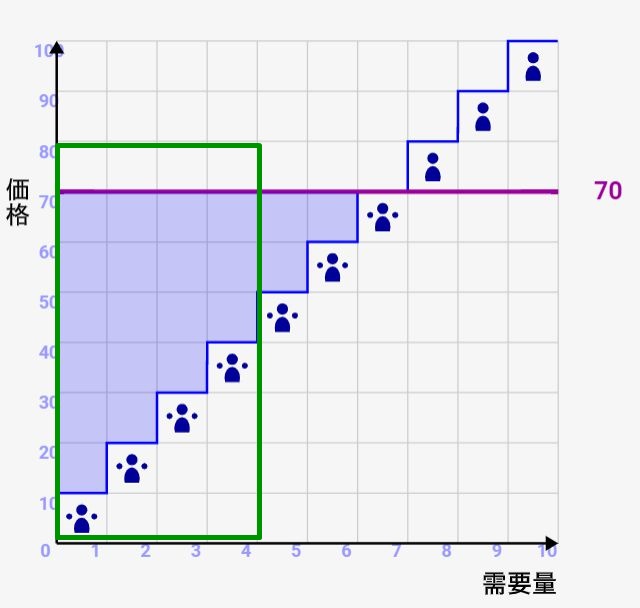
このように、社会的余剰を考えるときには、消費者と生産者の数と共に、さらに取引可能数を考慮しないといけないんですね！
　

シミュレーターを使って社会的余剰を理解しよう！

上記の社会低余剰を実際のシミュレーターを使って確認してみましょう！

シミュレーション結果考察

上記のシミュレーション結果を考察してみます。

価格によって、消費者余剰と生産者余剰のバランスが変わる

価格によって消費者余剰と生産者余剰のバランスが変わります。価格が上がると、消費者余剰が下がり、生産者余剰のバランスが上がっていきます。

消費者余剰・生産者余剰のバランスが悪いと、取引数が減り、社会的余剰が減少する

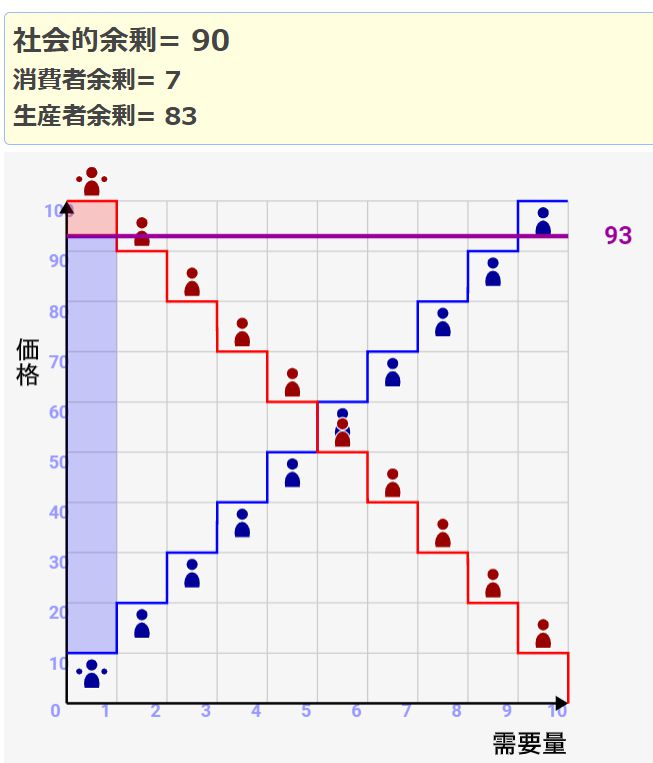
消費者余剰・生産者余剰のバランスが悪いと、全体の社会的余剰自体が減少します。シミュレーターの最大余剰は250ですが、バランスが悪いと↓のように90しか余剰が得られません。

価格が高いので生産者が有利なのですが、それによって取引数が減るので、生産者目線だけでもこの価格が最適ではないという事なんですね（生産者一人だけ嬉しく、他の人は得しない状態）

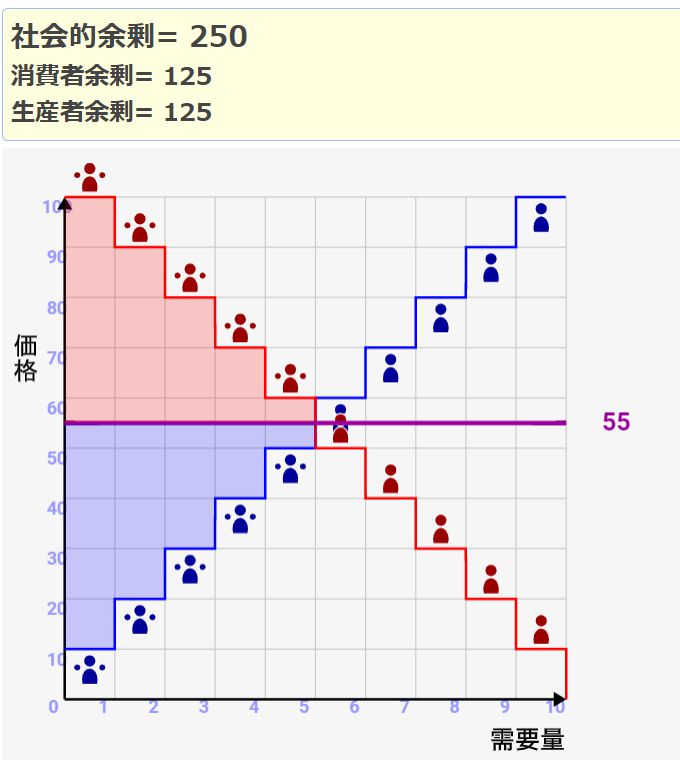
需要グラフと供給グラフがぶつかる交点あたりで、社会的余剰が最大になる

シミュレーターで実験してみると、社会的余剰が需要と供給の交点辺りで最大になるのが分かります。
　
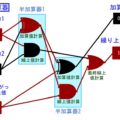
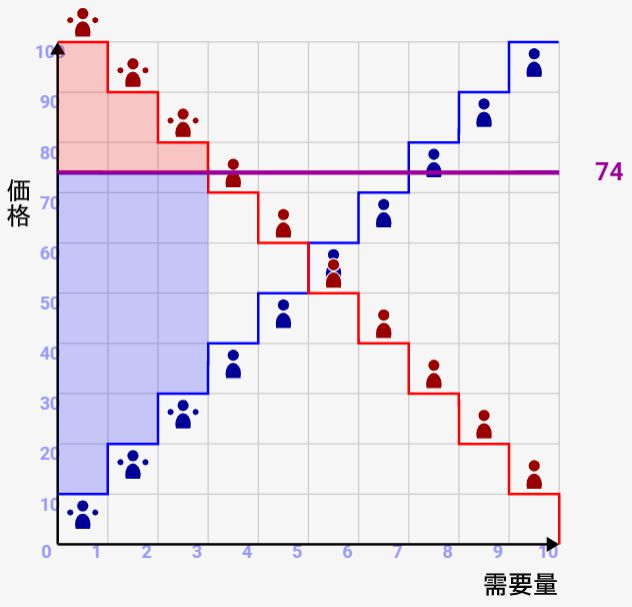
需要グラフと供給グラフが交わる地点で、社会的余剰は最大になります。その理由は↓のような絵を見ればわかるはずです。

↑のように、交点あたりの価格では全て需要グラフと供給グラフで囲まれた領域を全て塗りつぶすことが出来るんですね。余剰はこの領域内でしか生まれないので、「需要グラフと供給グラフが交わる地点が余剰最大化状態となる」わけです！
　
　
今回の考察で、「社会的余剰が最大化する場面」がわかりましたね。次回は、この社会的余剰が自然な市場でどのように最適化されていくかを見ていきます！
　

[関連記事] 経済学入門: 需要/供給と市場に関するシミュレーター

1．需要/供給と価格の関係

2．需要/供給から価格が決まる過程

3．需要と供給が変わった場合の価格/供給量の変動

4．需要と供給の価格弾力性

5．消費者/生産者の余剰

6．社会的余剰(本記事)

7．市場の自動余剰最適化、自由競争市場では自然に利益最大化される