「キルヒホッフの第2法則」が成り立つことをシミュレーションで理解しよう![物理入門]
前回記事で説明したオームの法則を用いて、様々な電気回路をシミュレート/解説していきます。
今回は前回のキルヒホッフの第1法則に続いて、「キルヒホッフの第2法則」についてのシミュレーターです!
![「キルヒホッフの第2法則」が成り立つことをシミュレーションで理解しよう![物理入門]](https://retu27.com/wp-content/uploads/20211107007069-500x437.png)
目次
おさらい:オームの法則
電源は、電位を上げて、より電流を流れやすくするものです。電位・電圧が高いほど、位置が高くなり、抵抗があっても電流を速く流せるようになるイメージです。

電圧・電位Vと、流れる電流I・抵抗Rの間には↓のような関係があります。これがオームの法則です!
\( \displaystyle \large V = IR \)
- V : 電圧[V]
- I : 電流[A]
- R : 抵抗[\(Ω\)]
複雑な回路の場合、、、どう計算すればよい?
基本的な、並列抵抗などの回路の計算方法は前回までで解説してきました。しかし、↓のような複雑な回路がある場合、単純には流れる電流を計算できません。

この場合には「キルヒホッフの法則」から方程式を導出して、解いていく必要があります。「キルヒホッフの法則」は2つあります。前回の第1法則に続いて、今回は「キルヒホッフの第2法則」を説明します!
キルヒホッフの第2法則
これは「各閉回路を一回転すると、電位の変化は0となる」という定理です。これは「通る経路が違っても、最終的に同じ地点なら同じ電位になるはず」という意味もあります。
↓例えばこのような閉回路(ループする部分)があったなら、
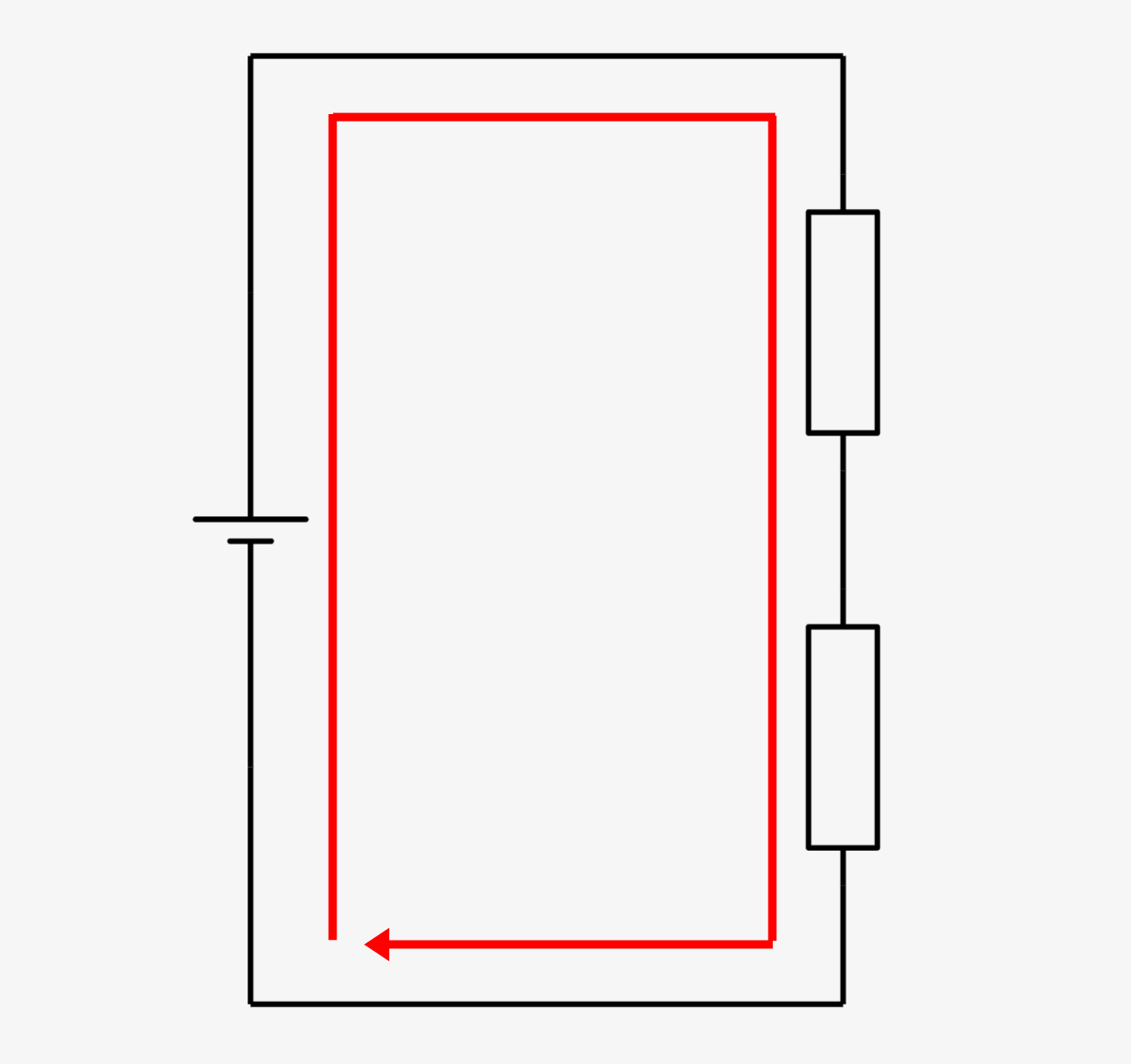
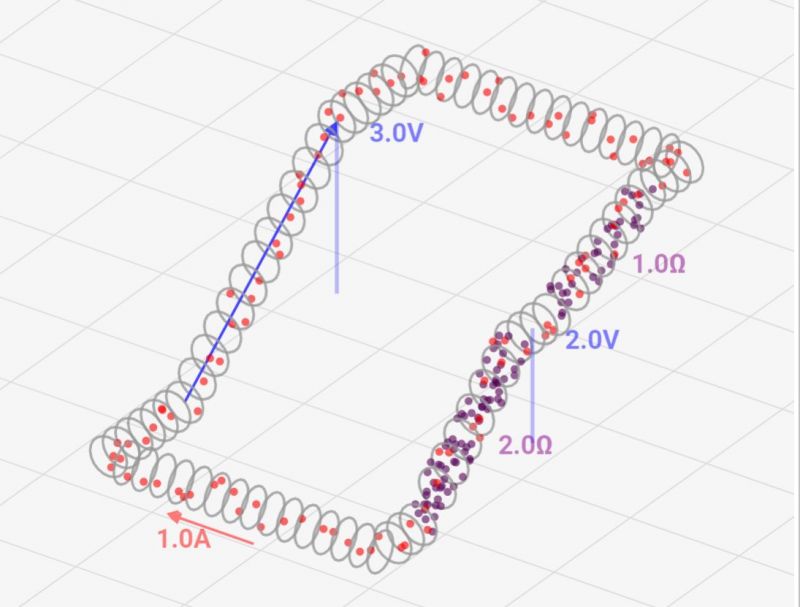
この各電位を高さで表現した場合、↓のようになるはずなんです。電池で電位が高くなっても、抵抗を通る度に電位が下がり、最後は元の電位=0と同じになるはずなんです。
[正常な回路]
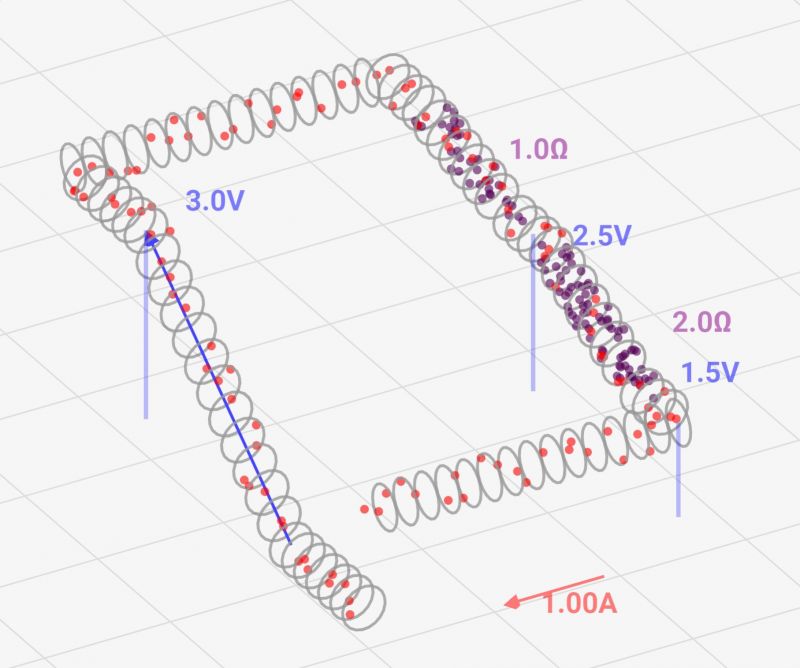
もし、この法則が成り立たないと、、、↓のような変な回路ができてしまいます。これだと、最初の電位よりも最後の電位が高くなってしまい、周回するたびに電位が高くなってしまうことになります。明らかにおかしいですよね。同じ地点ならば、一つの電位にならなければいけないのです!
[おかしい回路 同じ地点なのに電位差が出てしまう]
「キルヒホッフの第2法則」はあらゆる閉回路で成り立つ
「キルヒホッフの第2法則」は全体を一回転するときに成り立つだけでなく、回路内の閉回路で成り立ちます。
なので、↓のような複雑な回路の場合、赤線で引いた小さな閉回路(ループ部分)でも、「1周したときの電位差合計は0」ということが言えます。
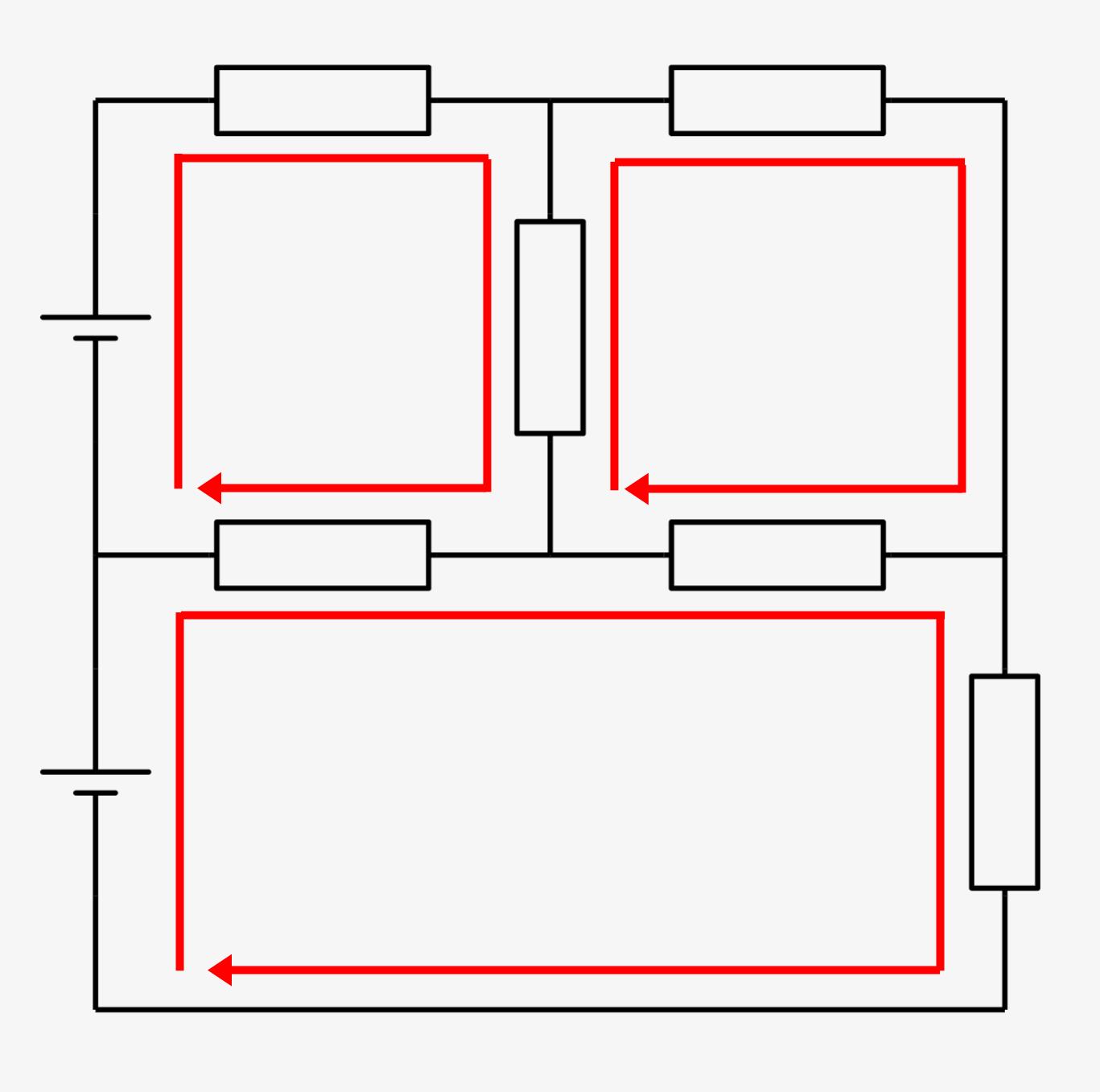
この法則が成り立たないと、、、先の例のように、同じ地点なのに電位差があるおかしな状態になってしまうんですね。
日常歩いてる道でも「キルヒホッフの第2法則」は成り立つ!
これは日常で私達が歩いてると道と同じです。どんな経路で歩いて上り下りしても、最終的に1周して元の位置に戻ったら、高さの変化の合計=0になるんです!電気回路にとって、電圧こそ高さに相当するものなので、全く同じことなんです。なので、「キルヒホッフの第2法則」はある意味で日常でも成り立つ当たり前のことを述べてるんですね。
一般的な定式
一般的な定式としては↓のように表せます。電位差を足していって、閉回路1周すると必ず電位差は0で元に戻ります。ループするときの向きを考慮する必要があることに注意して下さい!
閉回路内を1周するときの各電位変化を\(V_i\)とすると、↓が成り立つ
\( \displaystyle \large \sum_{i=閉回路}^{}(V_i) = 0 \)
「キルヒホッフの第2法則」の必要性をシミュレーターで確認しよう!
「キルヒホッフの第2法則」が成り立たないと、回路がおかしくなることを直感的に理解してみましょう!
今回は↓の回路を使い、↓のように左側を閉回路1,右側を閉回路2と名付けます。また、操作可能な抵抗を↓のようにR1,R2,R3と名付けます。
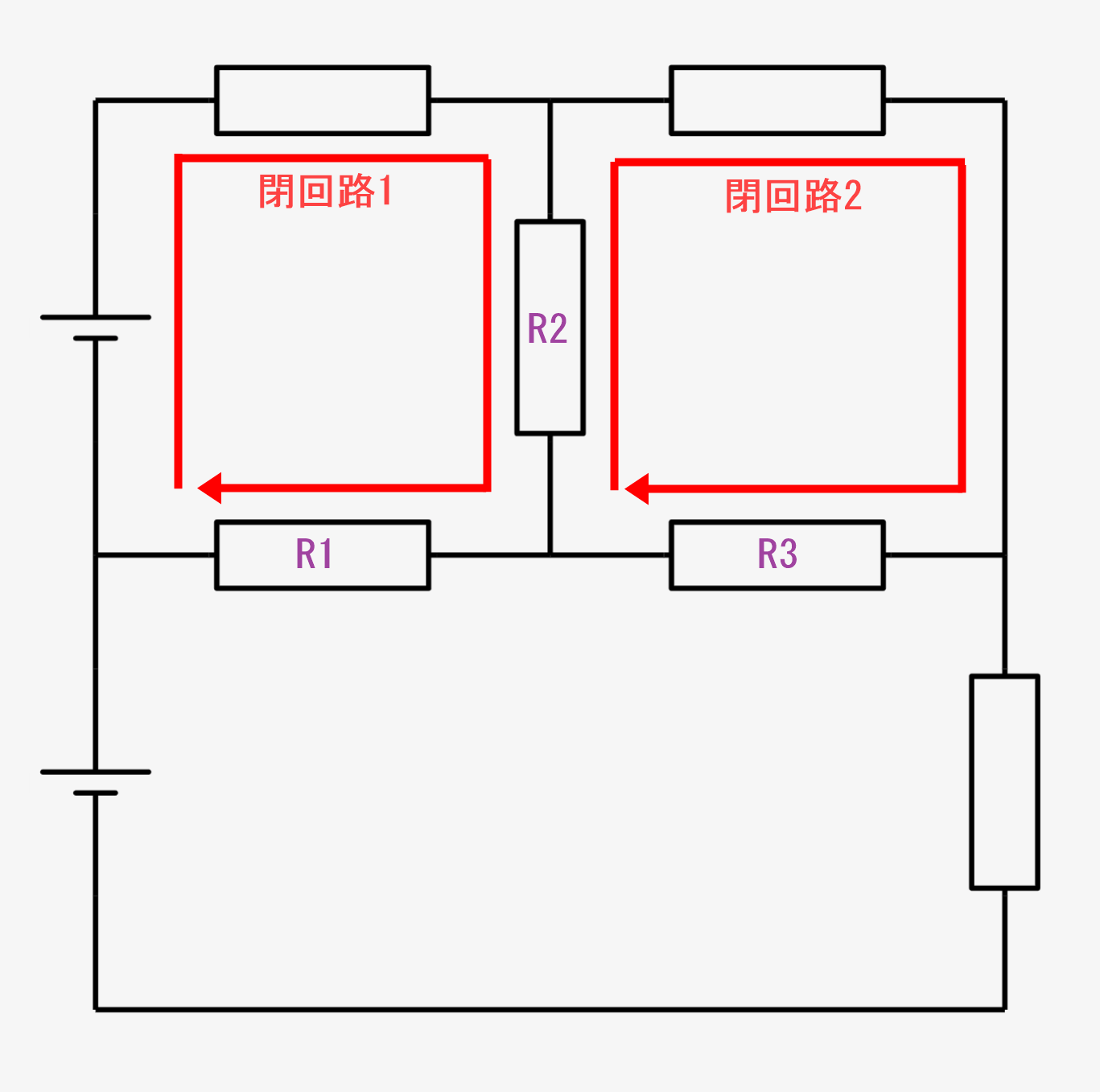
この上で、R1,R2,R3の電位差を変化させて、「キルヒホッフの第2法則」が成り立てば回路として成り立つことを確認してみましょう!
- ↑の回路図を3次元化したものです
- 高さは電位を表し、各分岐点で回路的につながっている必要があります
- その他の整合性については今は無視して下さい
- 電荷/電流はイメージとして流れてますが、厳密に計算したものでなないです。無視して下さい><
- スライドバーによって↑で名付けた3つの抵抗R1,R2,R3の電圧が変えられます
- 初期状態で「キルヒホッフの第2法則」が成り立つ状態になっています
- R1,R2,R3の電圧を変化させると、回路的におかしくなり、各閉回路の電位差合計が0でなくなり、「キルヒホッフの第2法則」が不成立になることを確認しましょう
- 初期状態以外でも「キルヒホッフの第2法則」が成り立つパターンがあり、閉回路の電位差合計1,2がともに0となることを確認しましょう
シミュレーター結果の要点
1R1,R2,R3の電位を変えてみると、初期状態以外でも「各閉回路の電位差合計=0」となるパターンがあることがわかります。例えば、↓のR1=2,R2=2.R3=0のパターンですね!
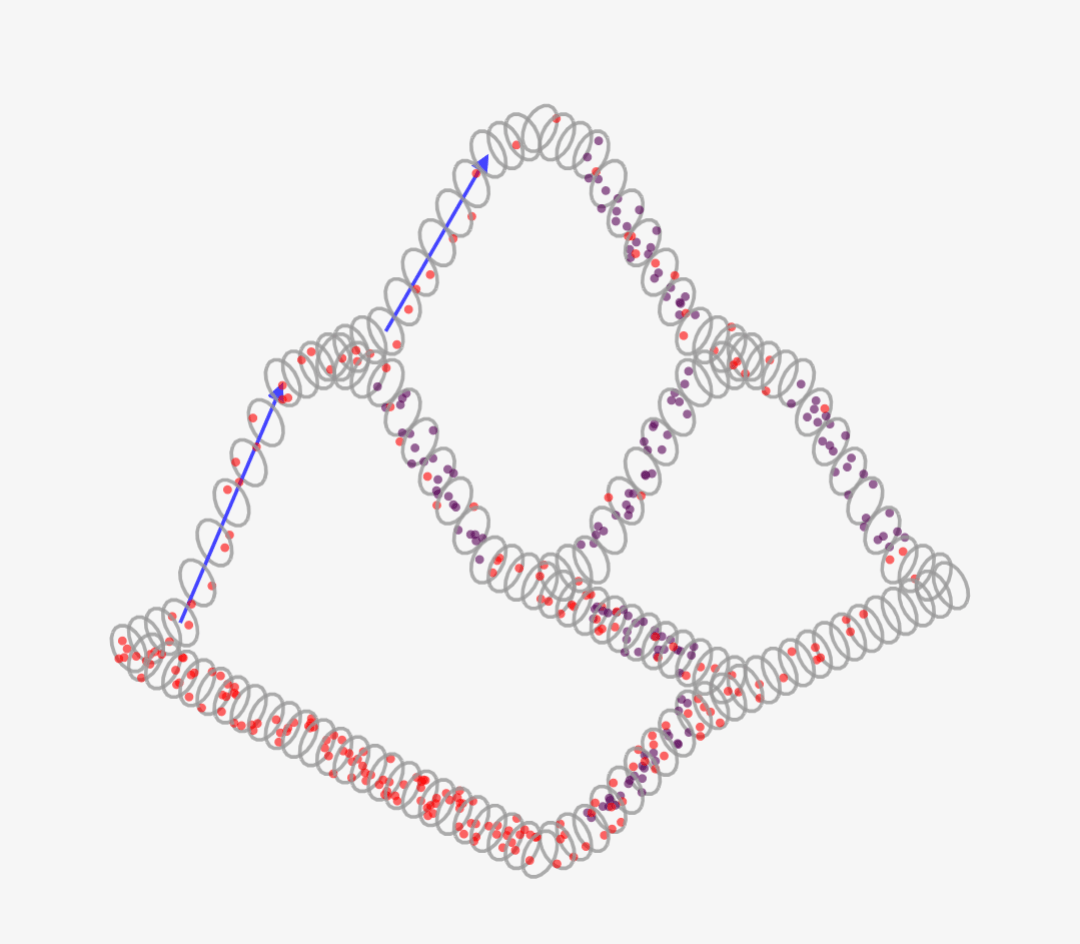
つまり↓の「キルヒホッフの第2法則」を適用しても、まだ自由度があるんです。ここから、さらに「分岐点の電流のin/out総計=0」という前回説明した「キルヒホッフの第1法則」を使うことで、はじめて一意に電位や電流を決定できるんです!
閉回路内を1周するときの各電位変化を\(V_i\)とすると、↓が成り立つ
\( \displaystyle \large \sum_{i=閉回路}^{}(V_i) = 0 \)
次回は、前回/今回説明した「キルヒホッフの第1法則」「キルヒホッフの第2法則」を使って、実際に複雑な回路の電圧・電流を解いて見ます!
- 電気回路の任意の経路を一周すると、必ず合計電位差は0になる
- キルヒホッフ第一法則と第二法則、両方使ってはじめて各経路に流れる電流が確定できる
⇒「電気回路・キルヒホッフの法則」カテゴリ記事一覧
その他関連カテゴリ














