「複雑な電気回路」をキルヒホッフの法則を用いて解く!シミュレーションで理解しよう![物理入門]
前回記事で説明したオームの法則を用いて、様々な電気回路をシミュレート/解説していきます。
今回は前回のキルヒホッフの第1法則に続いて、「キルヒホッフの第2法則」についてのシミュレーターです!
![「複雑な電気回路」をキルヒホッフの法則を用いて解く!シミュレーションで理解しよう![物理入門]](https://retu27.com/wp-content/uploads/20211107007072-500x491.jpg)
おさらい:オームの法則
電源は、電位を上げて、より電流を流れやすくするものです。電位・電圧が高いほど、位置が高くなり、抵抗があっても電流を速く流せるようになるイメージです。

電圧・電位Vと、流れる電流I・抵抗Rの間には↓のような関係があります。これがオームの法則です!
\( \displaystyle \large V = IR \)
- V : 電圧[V]
- I : 電流[A]
- R : 抵抗[\(Ω\)]
複雑な回路の場合、、、どう計算すればよい?
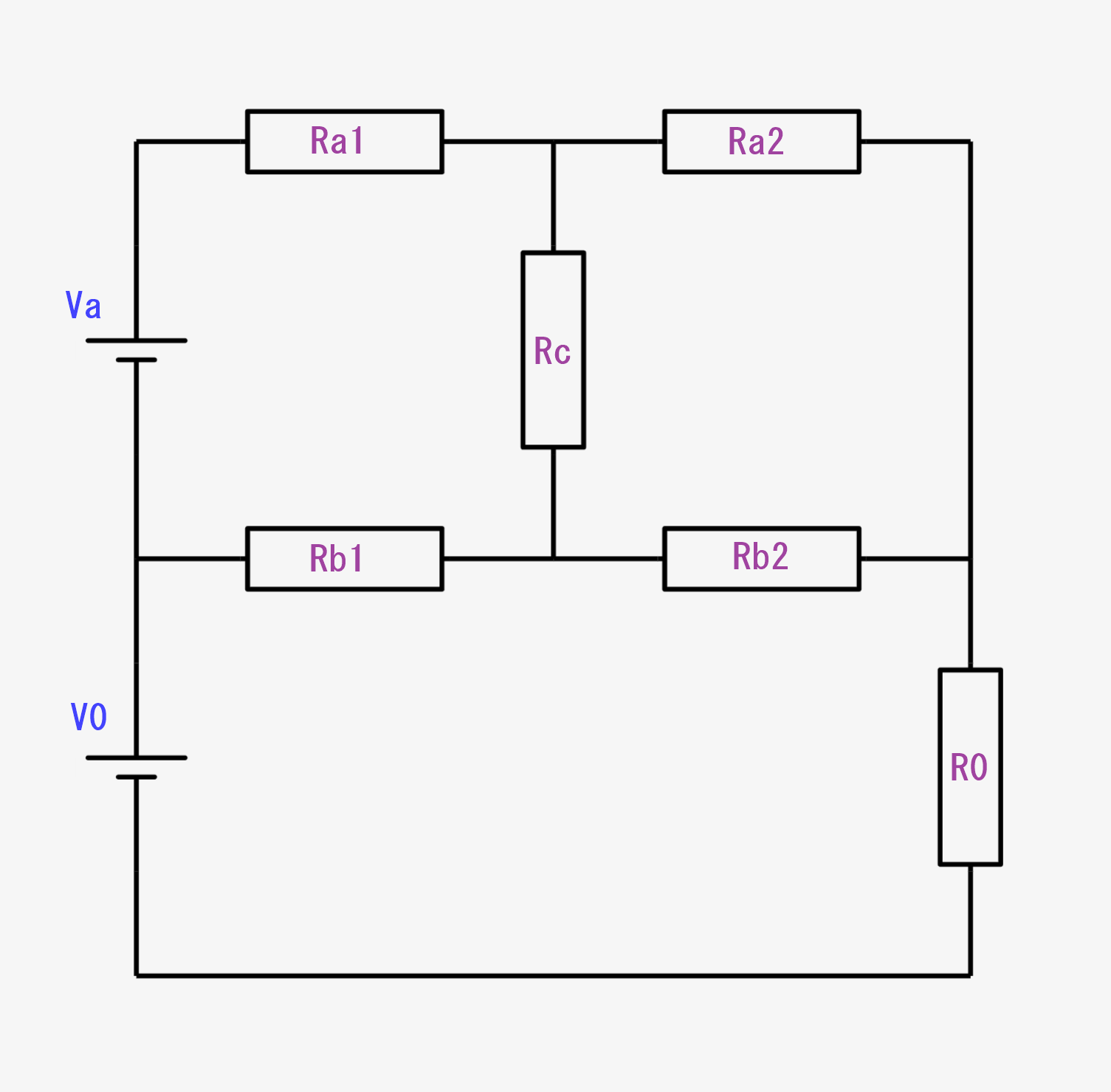
基本的な、並列抵抗などの回路の計算方法は前回までで解説してきました。しかし、↓のような複雑な回路がある場合、単純には流れる電流を計算できません。

前回までに「キルヒホッフの第1法則」「キルヒホッフの第2法則」について、解説しましたので、コレを使って解いていきます!
問題の解説
今、この回路に対して、↓のように電流の名前と方向を決定します。ただ、電流が必ずしもこの方向に流れるというわけでなく、「コチラをプラス方向にする」と決めるものです。(特に\(I_c\)は条件によってどっちに電流流れるか変わります)
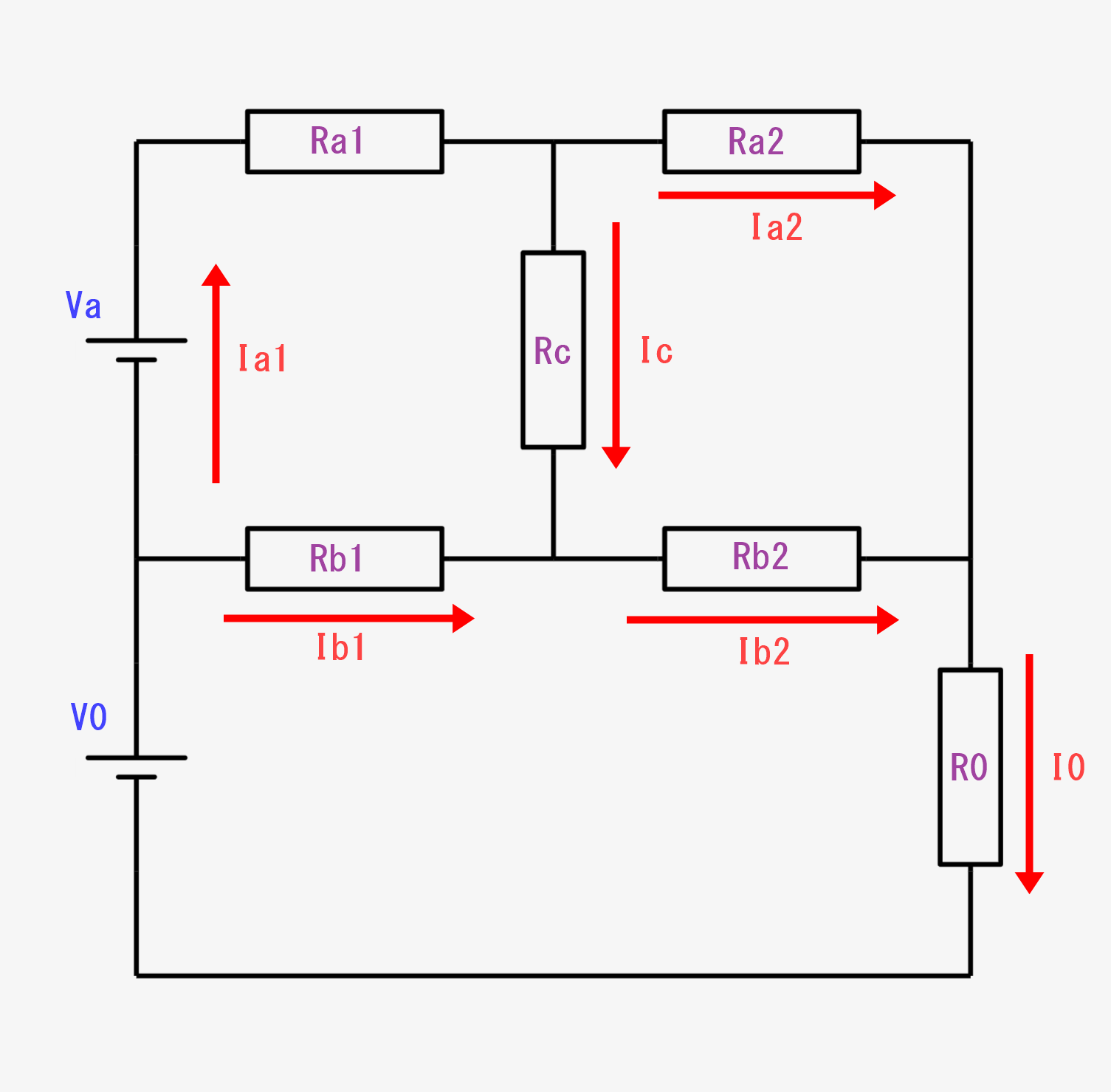
キルヒホッフの法則の適応
あとは、↑の図に従って、キルヒホッフの第1法則と第二法則で各点で定式化していくだけです。
各分岐点で、第一法則の「流入電流総和=流出電流総和」という条件をあてはめると、、、
\( \displaystyle I_0 = I_{a1} + I_{b1}\)
\( \displaystyle I_{a1} = I_{a2} + I_c\)
\( \displaystyle I_{b1} + I_c = I_{b2}\)
\( \displaystyle I_0 = I_{a2} + I_{b2}\)
さらに第二法則の「閉回路の電位変化の合計=0」を適応していくと、、、
\( \displaystyle V_0 + V_a – I_{a1} R_{a1} – I_{a2} R_{a2} – I_0 R_0 = 0\)
\( \displaystyle V_0 – I_{b1} R_{b1} – I_{b2} R_{b2} – I_0 R_0 = 0\)
\( \displaystyle V_a – I_{a1} R_{a1} – I_c R_c + I_{b1} R_{b1} = 0\)
\( \displaystyle I_c R_c – I_{a2} R_{a2} + I_{b2} R_{b2} = 0\)
という式が立てられます。電圧と抵抗によって、電流\(I_{a1},I_{b1},I_c\)が決まるものとして、この3つの値について解いていけば、、、、最終的に各地点でどれぐらいの電流が流れるかが求まります!(式を解くのは複雑なため、行列式などを活用すること推奨。後に解説予定)
なお、解いていくと\(I_c\)はマイナス値で求まることがあります。その場合は、反対方向に電流が流れているという事を示しているんです!
「複雑な電気回路」の必要性をシミュレーターで確認しよう!
「キルヒホッフの法則」を用いて、ここまで説明した↓回路図にどのように電流が流れるか確認してみましょう!

- ↑の回路図を3次元化したものです
- 高さは電位を表し、各分岐点で回路的につながっている必要があります
- 電源は青矢印で、抵抗は紫点部分で示しています
- スライドバーによって↑で名付けた各種電源の電圧,各種抵抗値が変えられます
- かなり複雑に状況変わるため、全パラメタを様々に動かしてみてどのように電流が変わるか確認してみましょう
- 特に電流Icの向きが状況によって、上向きになったり下向きになったり変化することを確認しましょう!
↑見たい角度に自由に表示・固定できます
- 複雑な回路は、キルヒホッフ第1法則とキルヒホッフ第2法則を使って解く
- 全ての閉回路や分岐点で式を作っていけば解ける状態になる
- ただし複雑な回路の場合、式が何個も出来上がるため、手で解くには大変になる(後に習う行列式を使えば、比較的楽に解ける)
⇒「電気回路・キルヒホッフの法則」カテゴリ記事一覧
その他関連カテゴリ















すべてのパラメーターを1.0にした際,シミュレーター上の図で計算が合わないと存じます。
(おそらく,0.25Aと0.75Aが小数第二位で四捨五入されて0.3A,0.8Aと表示されている)