積分の基礎！積分とは何？？[数学入門]

2021-04-22　 積分

ここまでの記事で、微分の基礎についてシミュレーターを用いて解説してきました。関数f(x)を微分するとは、f(x)の各点での「傾き」を表す導関数f'(x)を求めることでした。

積分とはその逆の操作になります。この積分について、まずは基礎中の基礎の部分をこの記事で解説していきます！

合成関数の微分の概念・イメージをシミュレーションで理解しよう！[数学入門]

2021-04-22　 微分の基礎

本記事では合成関数の微分について解説していきます。微分の基礎は、前回の記事でも説明しました。今回はその発展として、合成関数の場合にどのように微分するのかを解説します！
　
合成関数の微分は頻出する重大要素です。ただ公式を覚えるだけでなく、その意味やイメージを理解することがすごく重要なんです！

微分とは何か？「接線」と「その傾き」で定義を理解しよう！[数学入門]

2021-04-22　 微分の基礎

本記事から高校数学で一番重要と言える「微分」の考え方について説明します。微分は非常に分かりにくいものというイメージがあるかもしれませんが、その根本の意味を理解すれば、そこまで難しいものでは有りません。
　
ただ公式を覚えるだけでなく、その意味やイメージを理解することがすごく重要なんです！

「合成関数」をシミュレーションで分かりやすく理解！[数学入門]

2021-04-20　 関数

関数とは何か

数学の分野、その他の学問でも非常に重要な考え方に「関数」というものがあります。関数とは「ある値を入れたら、何らかの計算がなされて、別の値が返ってくるもの」です。関数を数式で表すと以下のようになります。

前回は「関数とは何か？」の基礎について解説しました。今回はその発展で「合成関数」について解説していきます！

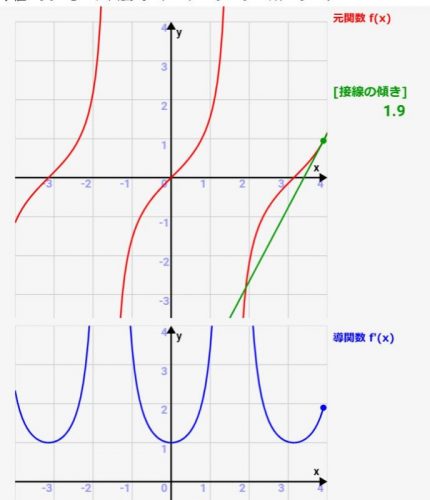
微分シミュレーター：三角関数(tan)の微分！関数とその導関数(微分)の関係をアニメーションで確認可！

2021-03-07　 微分シミュレーター

高校で習う微分、公式は習うのですが、実際にどういった関数グラフになっているかとか、元の関数との関係性が分かりにくかったりしますよね＞＜
　
微分(導関数)は「元の関数の各点での接線の傾き」を表したものです。ですので、元の関数の接線を描き、その傾きをグラフ化すれば微分(導関数)になっているんです！その関係性がわかるような、シミュレーターを実際に作ってみました！パラメタを変えると、どういった関数/導関数(微分)のグラフになるかをシミュレーターがすぐにアニメーション化してくれます！