「電気回路: 直列の抵抗」をシミュレーションで理解しよう![物理入門]
前回記事で説明したオームの法則を用いて、様々な電気回路をシミュレート/解説していきます!
今回は「電気回路: 直列の抵抗」についてのシミュレーターです!
![「電気回路: 直列の抵抗」をシミュレーションで理解しよう![物理入門]](https://retu27.com/wp-content/uploads/20211106007044-500x379.jpg)
おさらい:オームの法則
電源は、電位を上げて、より電流を流れやすくするものです。電位・電圧が高いほど、位置が高くなり、抵抗があっても電流を速く流せるようになるイメージです。

電圧・電位Vと、流れる電流I・抵抗Rの間には↓のような関係があります。これがオームの法則です!
\( \displaystyle \large V = IR \)
- V : 電圧[V]
- I : 電流[A]
- R : 抵抗[\(Ω\)]
「直列の抵抗」での計算の仕方
「直列の抵抗」とは↓の回路図のように、抵抗が縦に2つ並んだものです。
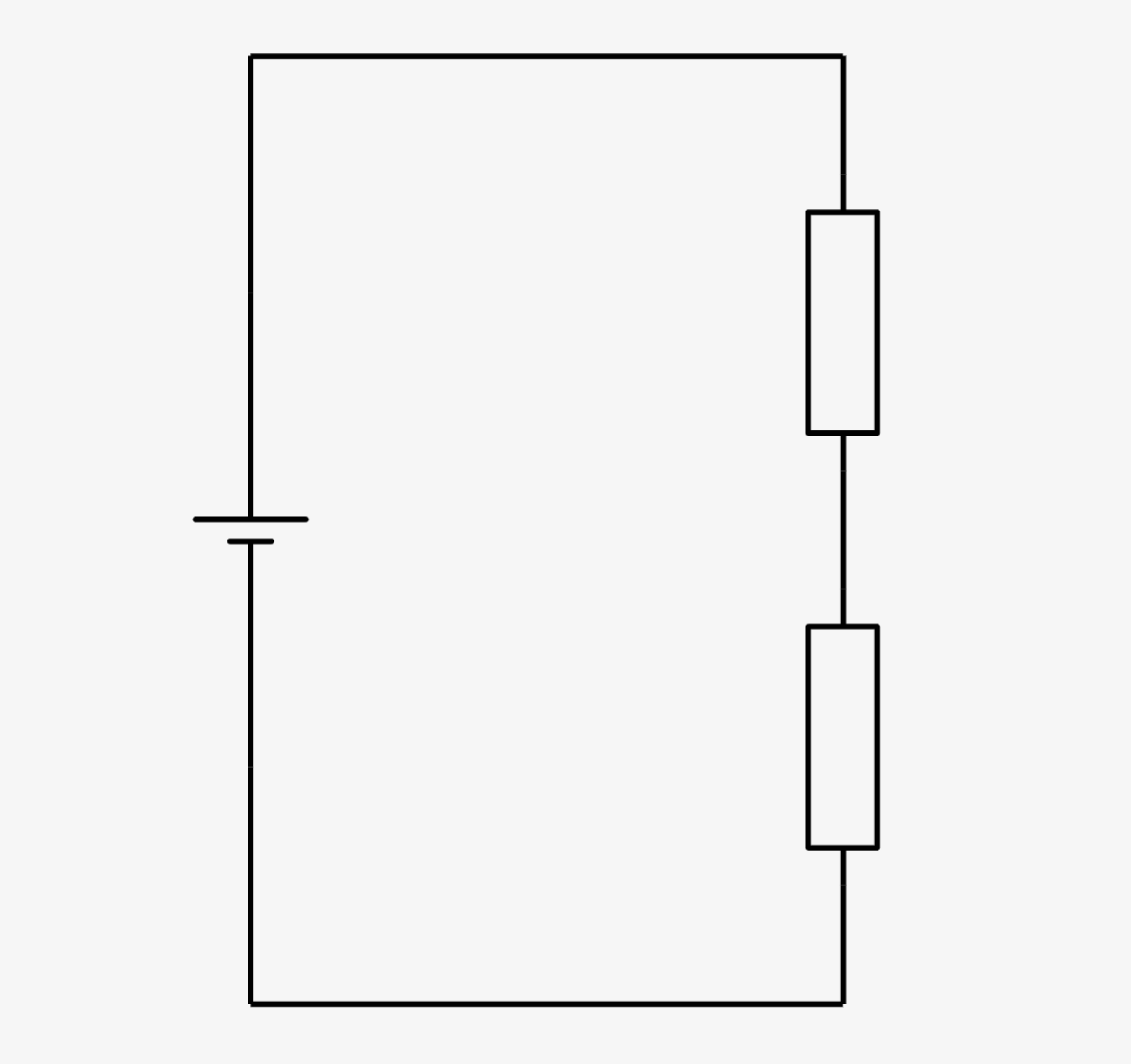
抵抗\(R_1\)と抵抗\(R_2\)の2つがあった場合、それを直列につないだ合成抵抗は↓のようになります。合成抵抗とは、2つの抵抗により実質的に一つの抵抗とみなした時の抵抗値です!
合成抵抗\( \displaystyle \large R = R_1 + R_2 \)
つまり、直列に抵抗を接続した場合、普通に抵抗値をを足した数が、合成抵抗になるのです。コチラのページで解説してますが、抵抗Rは抵抗の長さlに比例して抵抗値が増えます。2つの抵抗を足し合わせて、抵抗の長さを2倍になれば抵抗値も2倍になるはず。これは、↑の式でも合成抵抗:R + R=2Rという計算になり、あてはまるわけです!
抵抗値の比率によって、使われる電圧の配分が変わる
抵抗を超えることで、電源電圧によるエネルギーが消費され電圧が下がります。この時の電圧差異は↓のように抵抗値の配分により、決まります。抵抗値1Ωと抵抗値2Ωでは、電位の減少が1:2になります(高さで電位を表しており、紫色部分が抵抗です)
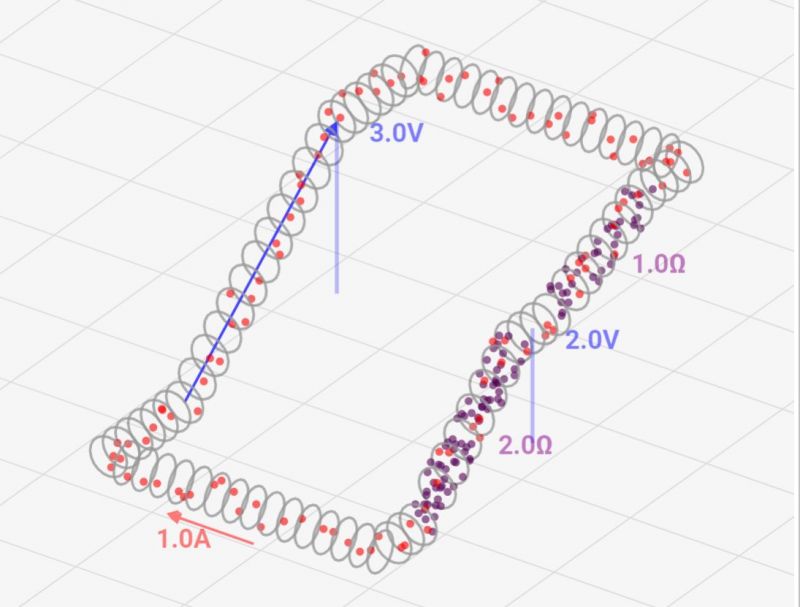
これは合成抵抗Rを使って、電流Iは↓のように求められるため、
\( \displaystyle \large I = \frac{V}{R} = \frac{V}{R_1 + R_2} \)
抵抗1,2での低下電圧\(V_1,V_2\)は以下のように求められるからです。↓式はまさに電源電圧Vを\(R_1\)と\(R_2\)の比率で配分してるものです!
\( \displaystyle \large V_1 = R_1 I = \frac{V R_1}{R_1 + R_2} \)
[抵抗2の低下電圧]
\( \displaystyle \large V_2 = R_2 I = \frac{V R_2}{R_1 + R_2} \)
「電気回路: 直列の抵抗」をシミュレーターで確認しよう!
それでは直列の抵抗による合成抵抗値の変化を、シミュレーターで確認してみましょう!
- 電源は青矢印で、抵抗は紫点部分で示しています
- 高さで各位置の電位の高さを表しています
- スライドバーによって2つの抵抗\(R_1,R_2\),電源電圧が変えられます
- 結果として、2つの抵抗が足し合わされ、最終的な合成抵抗が決まることを確認してみましょう
- 抵抗1,2の中間点の電位が、2つの抵抗値の比率で変わることを確認しましょう
- 直列の抵抗は、単純に足し算で求められる
- 各抵抗での低下電圧は、抵抗値の比によって決まる
⇒「電気回路・キルヒホッフの法則」カテゴリ記事一覧
その他関連カテゴリ














