バネによる力をシミュレーションで理解しよう![物理入門]
今回の記事から、バネによって物体にかかる力を解説します。バネの力には法則があるので、シミュレーターで理解してもらえたらと思います!
![バネによる力をシミュレーションで理解しよう![物理入門]](https://retu27.com/wp-content/uploads/rapture_20210411173736-1-500x196.jpg)
目次
フックの法則:バネによる力の法則
フックの法則とは
バネによる力は↓の有名なフックの法則に従うことが知られています。
バネによる力は、その伸びに比例する
例えば、↓の赤線部分がバネの自然長だとすると、4伸ばした時は↓のFのように力がかかります。
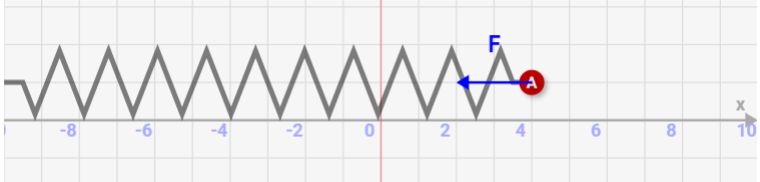
これを2倍の8伸ばすと、、、力も2倍になります!これがフックの法則です。
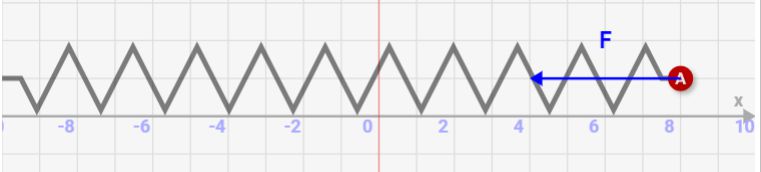
バネを縮めた時も同じように力は距離に従う
フックの法則が成立するのは、伸ばした時だけではありません。縮めた時も距離に比例します。
例えば自然長から4縮めた時、、、このときは4伸ばした時と同じ力が押す側に働きます。
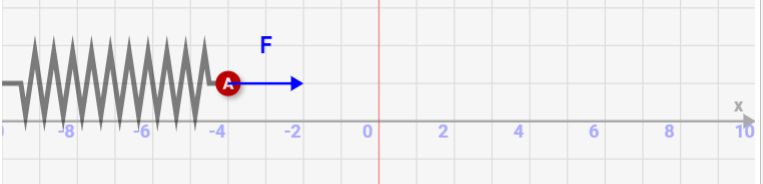
そして8縮めた時、、、↓のようにこれも押す力が2倍になります!

このバネの引いたり押したりする力を弾性力といいます!
バネの力の定式化
それでは、これまで説明したバネの力を定式化すると↓のようになります。
バネによる力 \(F = -kx\)
- k : バネ定数
- x : バネの自然長からの変位[\(m\)]
これは、伸ばしたり縮んだりする力がx=自然長からの距離に従うということを意味しています。
式の中で出てくるkはバネ定数(N/m)といい、バネの材質によって変わります。そして、そのバネを1m伸ばした時にかかるがkになることを意味しています。伸びにくいバネほど、このばね定数は大きくなり、大きな力がかかります。
力F = -kxと、マイナスがかかっているのはxの変位とは逆側に力がかかるからです。バネを伸ばすと縮む方向に、バネを縮めると伸ばす方向にと、逆側に力がかかるからです!
シミュレーターで「バネによる力」を理解しよう!
それでは上で説明した「バネによる力」をシミュレーターで実際に確認しましょう!式よりも、動かしたほうが分かりやすいですので
- スライドバーによって変位xとバネ定数kが変えられます
- バネの絵と同時に、バネによってかかる力Fの値も出力されます
- 変位xを変えると、その変位に比例して力が増すことを確認しましょう
- バネ定数kを変えると、それに比例して力が増えることを確認しましょう
↓スライドバーを変化させて実験してみましょう!
まとめ:バネには自然長からの変位に従った力がかかる
簡単にまとめです。今回解説したとおり、バネには↓のような力Fがかかります。
バネによる力 \(F = -kx\)
- k : バネ定数
- x : バネの自然長からの変位[\(m\)]
つまり、位置・変位に比例した力がかかるわけです!重力はどこでも一定ですが、バネはその変位によって力が変化するわけです。
このような性質によって、バネによって様々な運動が起こせます。そのあたりを次回以降の記事で解説していきます!
- バネはバネ定数kと変位に比例した力を働かせる
- 力の向きは変位と逆となる
⇒「単振動(バネ運動)」カテゴリ記事一覧
その他関連カテゴリ











コンデンサーの電荷移動のシュミレーションも作っていただきたいです!
ドップラー効果の同心円の広がりのシュミレーション分かりやすくて感動しました!
コンデンサーの電荷移動のシュミレーションも作っていただきたいです!