等速円運動を加速度は何故中心に向かう?シミュレーターで直感的理解を深めよう![物理入門]
前回の記事で、等速円運動の速度・加速度を微分で求めてみました。確かに微分でやると求められるのですが、少し直感的ではありませんでした。特に↓のように「速度は円の矢印」「加速度は中心に向かう矢印」となるのが直感的にわかりにくかったです。

そこで今回は、円運動の速度・加速度をちょ間的に理解できるようなシミュレーターを用意してみました!
目次
おさらい:等速円運動の速度・加速度は微分で求められる
まず前回のおさらいからです。等速円運動は↓のように定式化できます。
\( x \displaystyle = r \ cos(wt) \)
\( y \displaystyle = r \ sin(wt) \)
*初期角度はθ=0(rad)とする
- r : 半径[m]
- w : 角速度[rad/s]
これを微分すると↓のように速度と加速度が求められます。
\( v_x = (r \ cos(wt))’ = - rw \ sin(wt) \)
\( v_y = (r \ sin(wt))’ = rw \ cos(wt) \)
\( a_x = (- rw \ sin(wt))’ = - rw^2 \ cos(wt) \)
\( a_y = (rw \ cos(wt))’ = -rw^2 \ sin(wt) \)
今回はこれをもっと直感的に図的に求めてみます!
「速度=⊿位置/⊿t」で考えて、速度を求めてみる!
⊿tを使った速度の求め方
まずは速度からです。速度の定義は↓のようなものでした。
速度
\( \displaystyle = (\frac{移動距離}{時間}) = \frac{t+⊿t時点の位置 \ – \ t時点の位置}{⊿t} \)
つまり、t時点と(t+⊿t)時点の位置の差をとって、それを⊿tで割ればいいんです。正確な定義をすると、それを⊿tを物凄く小さくして0に近づけた値がその時点での速度といえるんです!
速度を求めるシミュレーター
上記の求め方を、シミュレーターでやってみましょう!
- ↓のスライドバーで円の半径と角速度(rad/s)、そして⊿tを自由に変更できます
- 画面にはそのt時点での位置(赤ボール)と、⊿t後の位置(黒点)が表示されており、その2つの差を使って↑の式で求めた速度を青矢印で表示しています
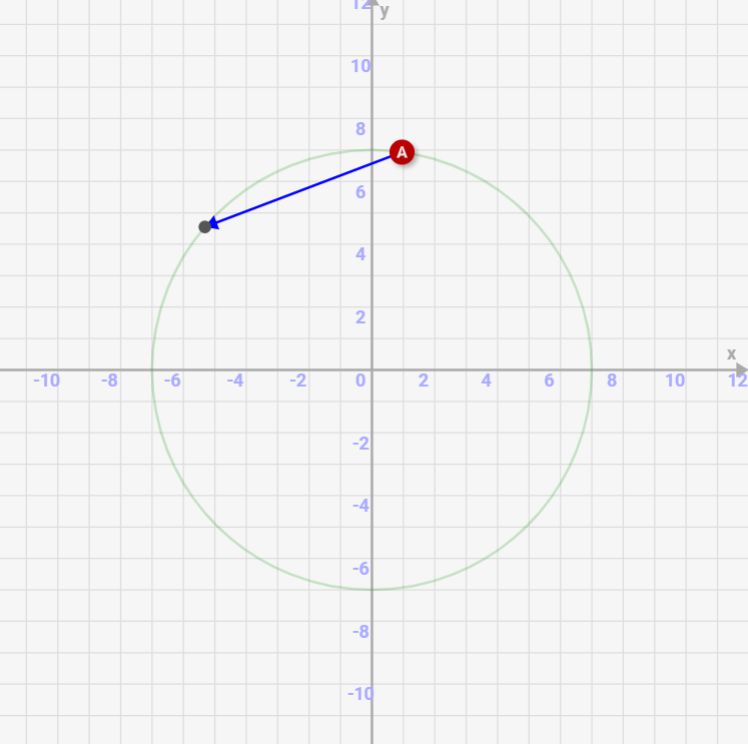
- ⊿tを1.0からどんどん小さくすると、速度は円の接線になることを確認しましょう
↓⊿tを小さくしていくと、速度は完全に円の接線となることを確認しましょう!
⊿tが小さくなると、完全に速度は円の接線となる
上記シミュレーターを使うと分かると思いますが
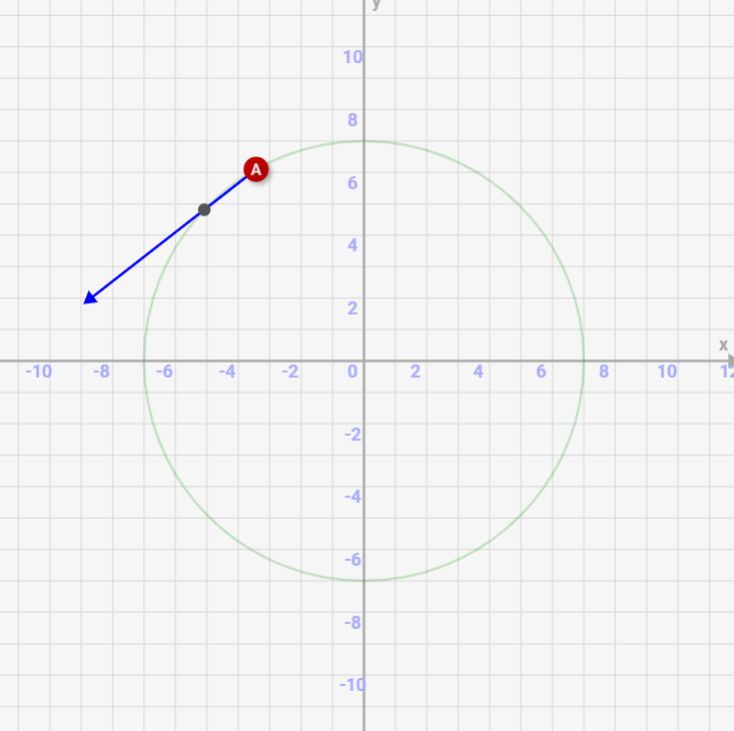
↓⊿t=1の場合、差が大きいので速度は接線から少しズレてます
↓⊿t=0.01の場合、差が極小になり、ほぼ接線になっています。
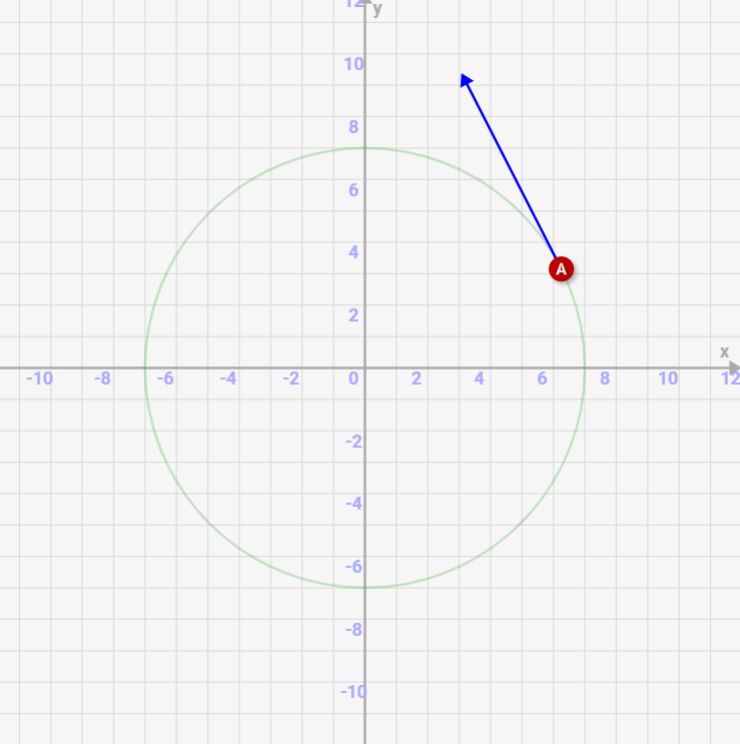
このように⊿tが0に向かうと、完全に「速度は円の接線と同じ向き」になるんです!
「加速度=⊿速度/⊿t」で考えて、速度を求めてみる!
上記の速度と同様に、加速度を⊿tを使って求めてみます!
加速度の定義は↓野通りです
加速度
\( \displaystyle = (\frac{速度の変化}{時間}) = \frac{t+⊿t時点の速度 \ – \ t時点の速度}{⊿t} \)
これも速度と同じく、⊿tを限りなく0に近づけていくと、t時点での加速度が求められます!
速度を求めるシミュレーター
上記の求め方を、シミュレーターでやってみましょう!速度と違って、図が少し複雑になります。
- ↓のスライドバーで円の半径と角速度(rad/s)、そして⊿tを自由に変更できます
- 画面にはそのt時点での位置(赤ボール)と、⊿t後の位置(黒点)が表示されています
- 2つの点の速度が青矢印(t時点)と緑矢印(t+⊿t時点)で表示されています
- 緑矢印と青矢印の差から↑の式を用いて計算した加速度を赤矢印で表示しています
- ⊿tをどんどん小さくすると、加速度は接線と垂直になり、中心に向かう線になることを確認しましょう
- 速度の差分の計算を分かりやすくするため、原点中心に青/緑矢印を表示しています(同じ色の矢印は、全て同じ向きになっています)
↓⊿tを小さくしていくと、加速度は中心に向かう線になることを確認しましょう
シミュレーター結果解説
少し分かりにくいのでシミュレーターの結果の解説をします。
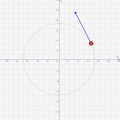
まず⊿t=1のとき。この時は青矢印(t時点の速度)と緑矢印(t+⊿t時点の速度)の差が激しい為、その差の赤矢印(加速度)も少しズレた方向にいっています。
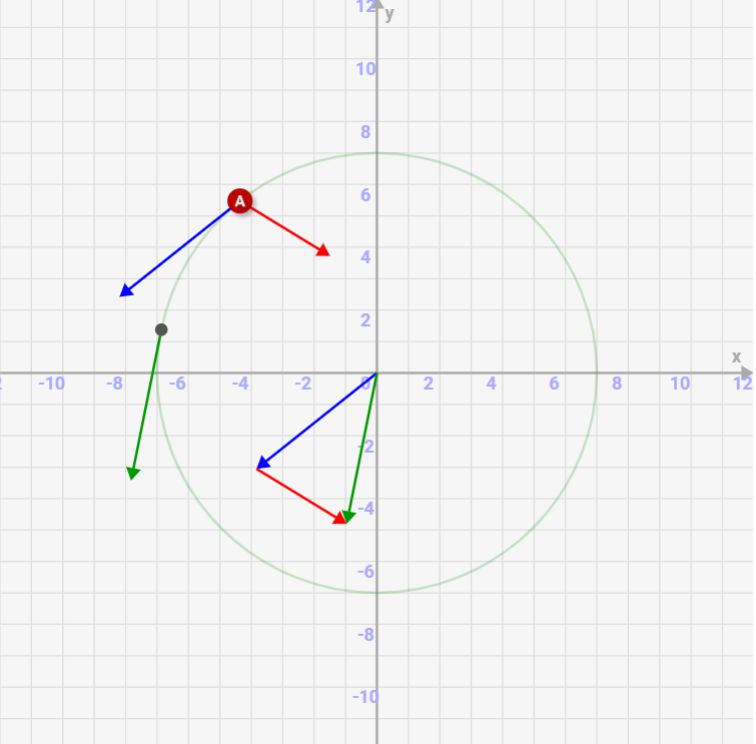
⊿t=0.3のとき。だいぶ青矢印と緑矢印の差がなくなり、その差から計算した加速度も中心に近いとこをさしています
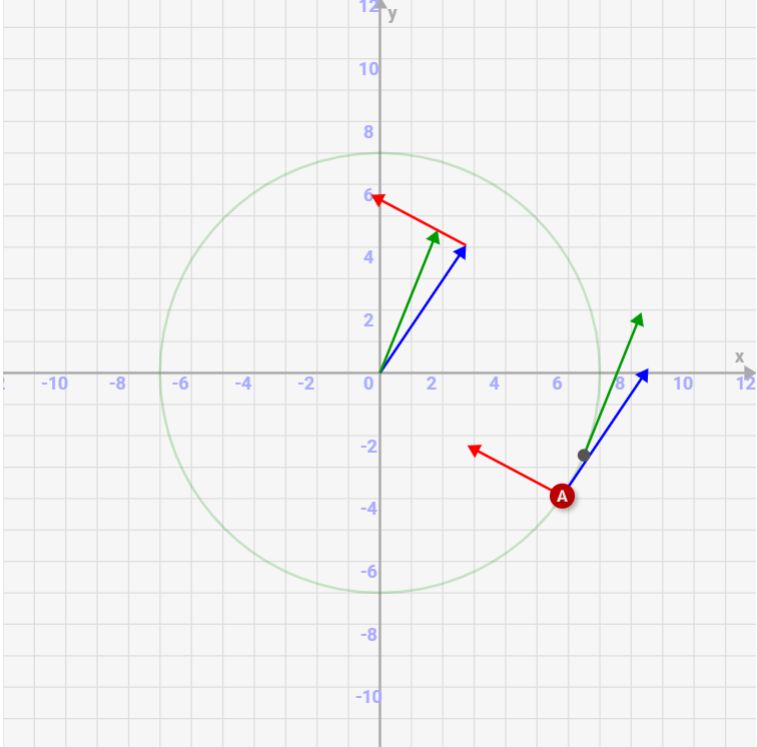
⊿t=0.01のとき。もはや青矢印と緑矢印は一致しており、赤矢印で示す加速度も中心に向かっています!
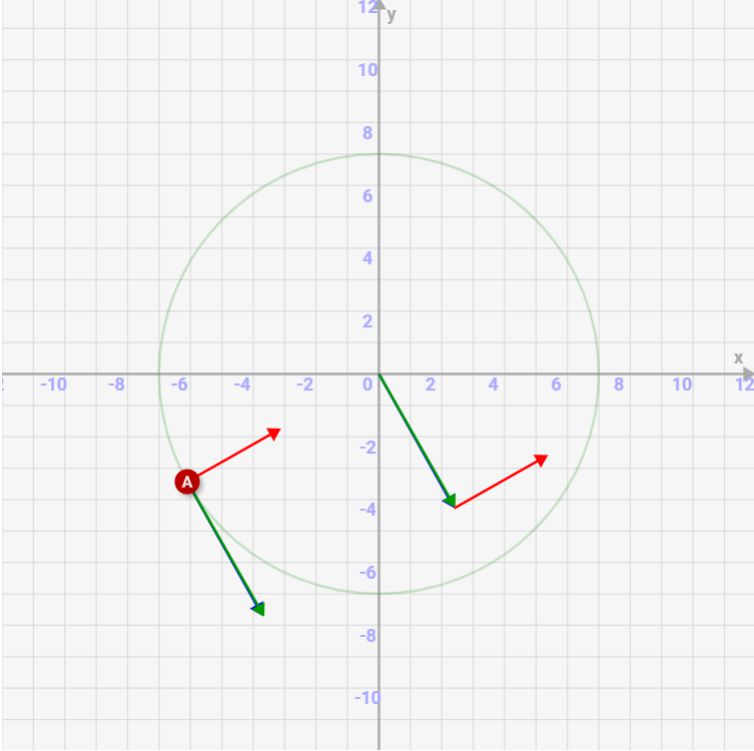
このように、⊿tを小さくすると、加速度が中心にむかっていくことが分かります!
まとめ:微分に頼らずに、⊿tを使っても速度・加速度は求められる
上記の論議の通り、速度/加速度は⊿tを使って求めていくと、直感的にも「速度は円の接線向き」「加速度は中心に向かう向き」にいくのがわかると思います!
微分で求めた方が楽ですが、このような考察も大事です!是非、このイメージをつかんでおきましょう!
- 円運動の速度は、円の接戦方向となる
- 円運動の加速度は、円の中心に向かう
⇒「円運動」カテゴリ記事一覧
その他関連カテゴリ