積分の意味をシミュレーターで理解しよう!積分は「lim Σf(x)*⊿x」と考えられる![数学入門]
前回の記事までで、積分の基本的な考え方について説明しました。「積分は微分の逆演算」という定義で、積分の考え方を解説しました。
しかし、その他にも積分の考え方・見方があるんです!今回は「接線の傾きをかき集める」という考え方を、シミュレーターを用いて示していきたいと思います!
![積分の意味をシミュレーターで理解しよう!積分は「lim Σf(x)*⊿x」と考えられる![数学入門]](https://retu27.com/wp-content/uploads/rapture_20210506222322-465x500.jpg)
目次
「微分値は原始関数の接線の傾き」これを利用して、関数の近似を求める
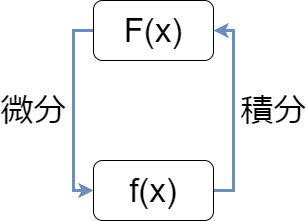
原始関数F(x)の接線の傾きがf(x)となる
積分の意味は、「微分と逆演算をして、f(x)の原始関数F(x)を求める」です。逆にいうと、「求めようとしている原始関数は、微分するとf(x)になる」んです。これまでも解説してきたとおり、f(x)はF(x)の接線の傾きの値となるんです。
関数F(x)の増加分の近似を考える
ここで、「関数の接線の傾き」と「関数の値」の関係を考えます。実は、十分に小さい⊿xをもってくると、↓の式が成り立つんです。
⊿y=F(x+⊿x) – F(x) ≒ f(x)*⊿x
これは、こちらの合成関数の微分で示した考え方です。
↓大きな視点でみると関数(赤線)と接線(緑線)は大きくズレていますが、、
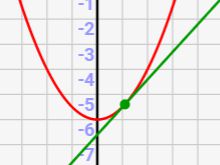
↓⊿xとミクロな世界でみると、接線と関数はほぼ重なりあっています。これは微分可能な関数が連続であるという性質から、必ずこうなります。

ここで、↓のように接線に合わせて⊿xと⊿yを定義することを考えます。
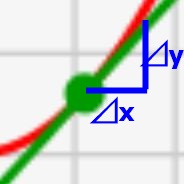
すると、「接線の傾き=F'(x)=f(x)」なので↓の公式が成り立ちます。xが⊿xだけプラスされた時、⊿y=傾き*⊿xだけ伸びるんですね。
これが十分小さい⊿xで関数F(x)の伸びと同値になるので、↓の近似が成り立つわけです!
⊿y=F(x+⊿x) – F(x) ≒ F'(x)*⊿x
定積分を近似してみる
積分をシグマ形式で表す
それでは次に、定積分の近似を考えてみます。↓のようにx=α~βの定積分を考えます。
\( \displaystyle \int_α^β f(x) dx\)
上記の「⊿xで細かく分割する」という考え方を適用することを考えます。αからβを細かく分割することを考えます。すると、
\( ≒ f(α)*⊿x + f(α+⊿x)*⊿x + \)
\( f(α+2⊿x)*⊿x + … + f(β)*⊿x\)
\( \displaystyle = \sum_{x=α}^β f(x)*⊿x\)
というように、⊿xで小さく分割することで、積分をシグマの形式で表すことができるのです!
極限をとって、積分と同値にする
上記の式はあくまで近似です。しかし⊿xを無限に小さくしていくと、f(x)と同値になるんです!
\( \displaystyle \int_α^β f(x) dx\)
\( \displaystyle = \lim_{ ⊿x \to 0 } \sum_{x=α}^β f(x)*⊿x\)
このように考えると、積分というのは「xを⊿xと細かく区切って、f(x)と乗算して総和をとる演算」とも言えるんです!ただし、⊿xは無限に0に近づける必要があるので、そこは注意です。
補足:積分区間をn等分すると考える
上記のように、積分はシグマ形式で表すことができます。↑では⊿xで分割しましたが、もっとわかりやすく「α~βをn等分して足していく」と考えます。⊿x=\(\frac{β – α}{n}\)として、nを無限に大きくしていくことを考えます。すると、↓の形式で表すことができます。
\( \displaystyle \int_α^β f(x) dx\)
\( \displaystyle = \lim_{ n \to ∞ } \sum_{k=0}^{n-1} f(x_k)*\frac{β – α}{n}\)
* \( x_k = α + (β – α)*\frac{k}{n} \)
これは、別記事で説明しますが、区分求積法という表現になります!!↓のシミュレーターではこの結果を用います!
定積分シミュレーター!定積分のイメージを「Σf(x)*⊿x」という観点で、理解しよう!
シミュレーターの説明
上記で説明した積分をシグマで計算するイメージを、シミュレーターで確認してみましょう!「⊿y=f(x)*⊿x」を毎回計算して、足し合わせるイメージです。
の各パラメタa~cを↓のスライドバーで変更すると、それを積分して原始関数F(x)が計算されます。また、シミュレーター上でそのF(x)の形状がグラフ化され、定積分の値が出力されます。
今回はそれと同時に、x=α~β区間をn等分して、「⊿y=f(x)*⊿x」を計算します。そして、「接線から計算した⊿yと実際のF(x+⊿x) -F(x)との差分」を↓のように紺色で図示します。紺色の縦線が小さいほど、実際のF(x+⊿x) -F(x)と誤差が少なく、F(x)の近似に近いといえます。
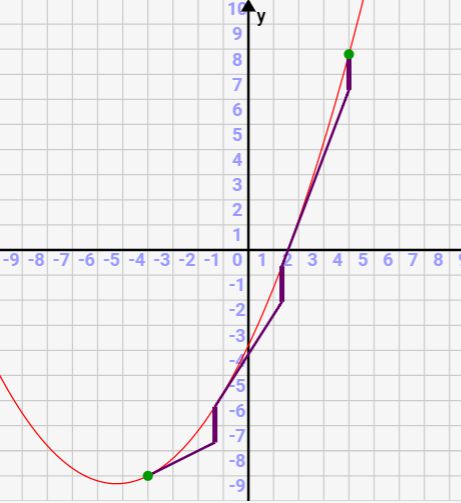
実際の積分値とシグマによる近似値を↓のように並べて表示するので、分割数nが大きくなるほど、積分値と近似値が近くなることを確認しましょう!

定積分シミュレーター
↓のスライドバーでf(x)の関数や、積分区間α~βを調整した後、分割数nの値を上げてみましょう!
↓nが大きくなるほど、積分値(上)とシグマ近似値(下)が近くなることを確認しましょう!
\( {f(x)=} \) + 1\( {x^2 } \) + 1\( {x } \) + 1
\( {F(x)=} \) + 1\( {x^3 } \) + 1\( {x^2 } \) + 1\( {x } \) +C
= 0.0
= 0.0
シミュレーター結果の考察
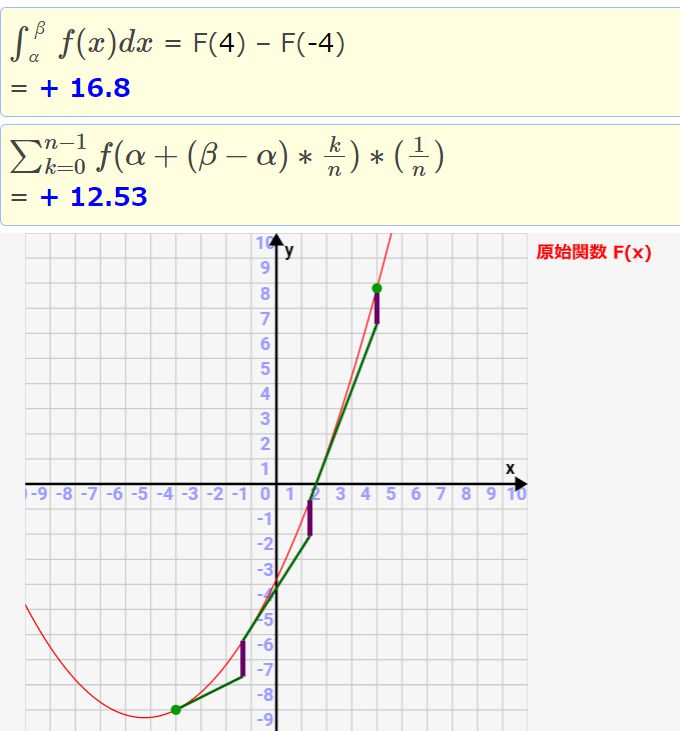
例題として下のようにF(x)が二次関数になる場合で、n=1 → 100まで上げていったときの動きを確認しましょう。
n=1の場合。接線と関数F(x)との差が大きく、誤差がとても大きいです。
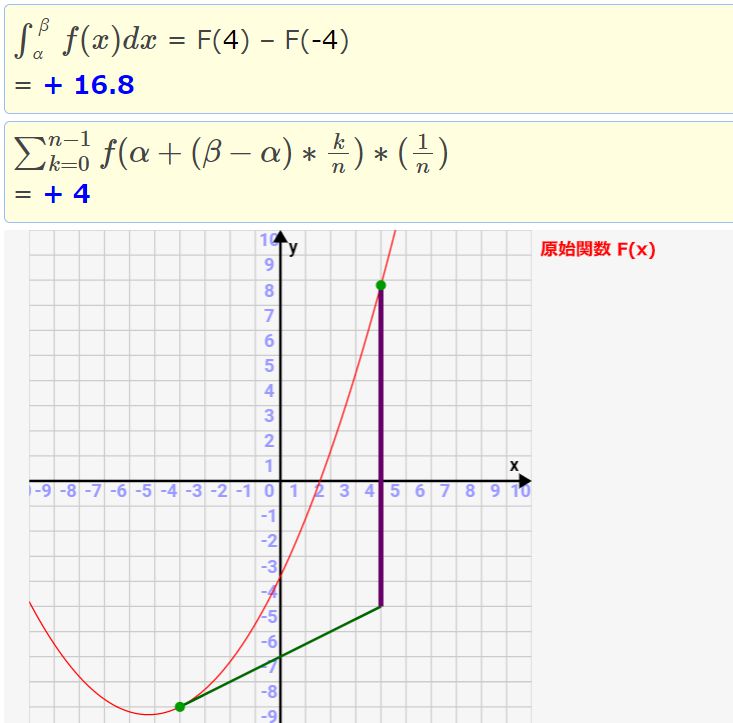
n=15の場合。もはや人間の目だと関数とシグマによる近似は同じようにしか見えません。
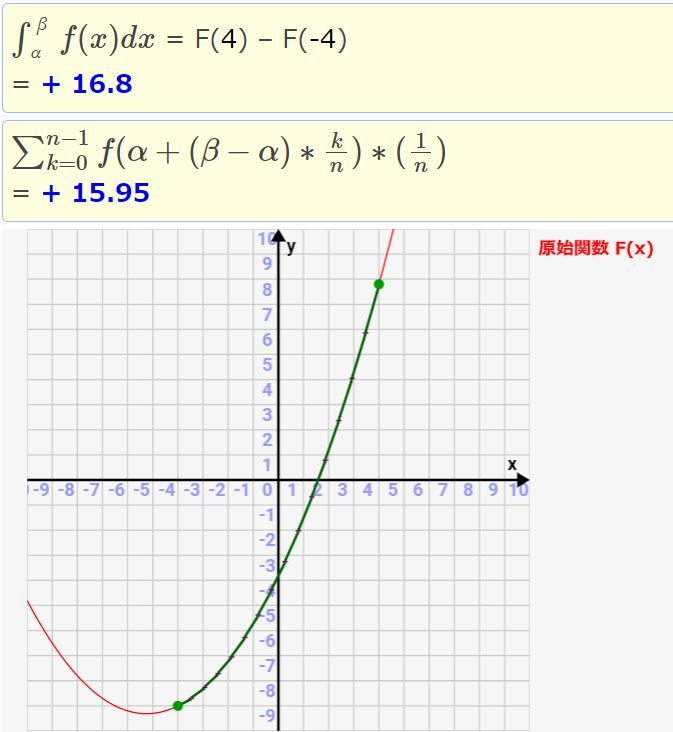
n=100の場合。もはや同一にしか見えません。しかし、積分値とシグマ近似値には0.1の誤差がまだありますね。
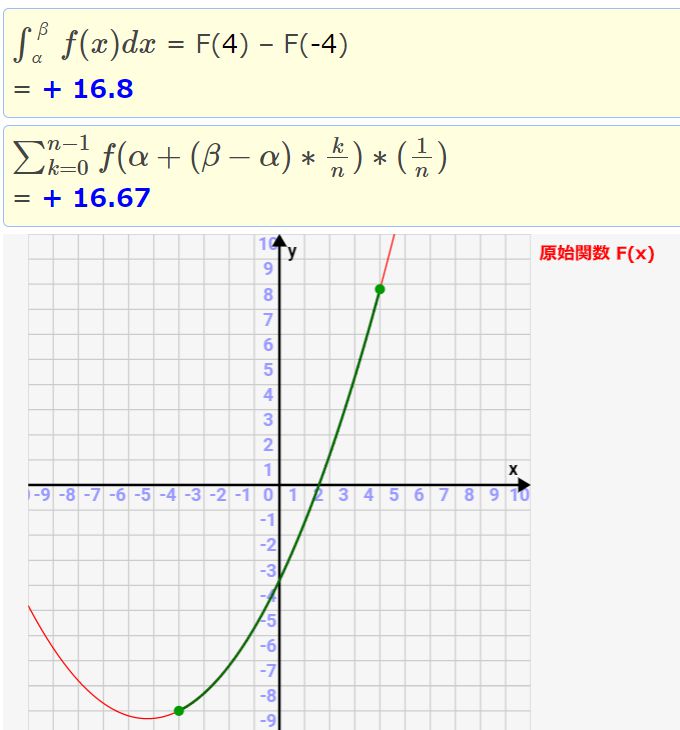
実際の積分では、これをn=100どころでなく、無限にまで上げていきます。すると、「積分値=シグマ計算値」となるのです!
積分を「lim Σf(x)*⊿x」というイメージで考えられるようにしよう!
今回は、前回まで解説してきた積分について、別の視点から考察してみました。微分とは、その関数の接線の傾きを求めることです。そして、その「接線の傾き」と「微小量⊿x」を用いると、積分は↓のようにシグマで表すことができるようになるんです!
\( \displaystyle \int_α^β f(x) dx\)
\( \displaystyle = \lim_{ ⊿x \to 0 } \sum_{x=α}^β f(x)*⊿x\)
微分と積分は無限に小さくしたりする演算なのでイメージしにくいです。それに対して、絵で見えるような「lim Σf(x)*⊿x」というイメージは重要です。積分を考える時には、このイメージに立ち返りましょう!
⇒「積分」カテゴリ記事一覧
その他関連カテゴリ