基本的な積分の求め方(n次関数)&線形性をシミュレーターで理解しよう![数学入門]
前回の記事で、積分の基本的な考え方について説明しました。積分は微分とは逆演算で、「傾き」から元の関数を推定する演算なのです。
今回は簡単な実例を用いて、積分や元の関数の求め方を解説していきます!
![基本的な積分の求め方(n次関数)&線形性をシミュレーターで理解しよう![数学入門]](https://retu27.com/wp-content/uploads/rapture_20210423203804-319x500.jpg)
n時間数の積分
このページでは一番分かりやすい実例として、n次関数の積分について考えてみます。
まず、n次関数の微分については、コチラのページの通り、↓のような公式があります。
\( (x^n)’ = nx^{n-1}\)
例をあげると\( (x^3)’ = 3x^2\)であり、\( (x^2)’ = 2x\)ということです。
逆にこのn次関数を積分したい場合はどうすればいいのか、、、というと、実はただ上記の公式に当てはめるだけなんです!上記公式から、逆に考えると
が成り立つことがわかります。積分は逆演算なので、こうなるわけです。
ここから、この両辺を(n+1)で割ると、、、
\( \int x^{n} dx = \frac{1}{n+1}x^{n+1} + C(積分定数)\)
となります。これこそがn次関数の積分公式です!積分の場合は(n+1)で割って、次数を1つ上げればOKなんです!
このように、微分と逆演算して求めた関数を原始関数と呼びます。
f(x)を微分したものを導関数といい、f'(x)という記号で表します。それと逆にf(x)を積分したものは原始関数とよび、F(x)と大文字にして表します。この関係性をまとめると↓の通りです。

積分の線形性
ここで重要な法則があります。積分の線形性です。線形性とは↓のような性質です。
\( \int f'(x) + g'(x) dx= F(x) + G(x) + C\)
\( \int Af'(x) dx= AF(x) + C\)
これは微分演算で線形性があることからも自明です。原始関数をA倍したら、その微分である導関数もA倍になります。また、項が別れていたら微分は別々に演算できるので、積分でも同様です。
この線形性があるので、例えば
は線形性を使って、↓のように演算できます。
↓線型性1による分解
\( \displaystyle = \int 2x^3 dx + \int 3x^2 dx + \int x dx + \int 3 dx dx \)
↓線形性2によって、係数を前に出す
\( \displaystyle = 2\int x^3 dx + 3\int x^2 dx + \int x dx + 3\int 1 dx \)
↓公式適応、積分定数付加
\( \displaystyle = 2\frac{1}{4}x^4 + 3\frac{1}{3}x^3 + \frac{1}{2}x^2 + 3x +C \)
\( \displaystyle = \frac{1}{2}x^4 + x^3 + \frac{1}{2}x^2 + 3x +C \)
このように、微分と同じく線形性を用いて別々に演算出来るんです!
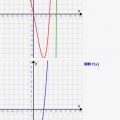
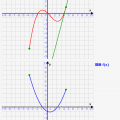
積分シミュレーター!積分のイメージを理解しよう!
上記のn次関数の多項式の場合について、シミュレーターを用いて考察してみましょう!このシミュレーターでは導関数
の各パラメタa~dを変更すると、それに合わせて原始関数F(x)が計算されます。また、シミュレーター上でその形状がグラフ化されます。
f(x)の係数を変えて、原始関数F(x)が計算される過程を確認しましょう!
\( {f(x)=} \) + 1\( {x^3 } \) + 1\( {x^2 } \) + 1\( {x } \) + 1
\( {F(x)=} \) + 1\( {x^4 } \) + 1\( {x^3 } \) + 1\( {x^2 } \) + 1\( {x } \) +C
↓値を変えると、自動的にアニメーションが始まります!
↑動的に再生速度を変えられます。左端で0にすると、一時停止となります。
まとめ:積分は微分とは逆演算だけど、クセがある><
最後にまとめです。今回は積分の基礎的な演算について解説しました。
もっとも基本的な演算であるn次関数の積分は↓のようになります。
\( \displaystyle \int x^{n} dx = \frac{1}{n+1}x^{n+1} + C(積分定数)\)
この公式と積分の線形性を使うと、多くの多項式を一発で積分できます。ぜひ、↑のシミュレーターを使ってこの積分のイメージを理解しましょう!
⇒「積分」カテゴリ記事一覧
その他関連カテゴリ