積分の基礎!積分とは何??[数学入門]
ここまでの記事で、微分の基礎についてシミュレーターを用いて解説してきました。関数f(x)を微分するとは、f(x)の各点での「傾き」を表す導関数f'(x)を求めることでした。
積分とはその逆の操作になります。この積分について、まずは基礎中の基礎の部分をこの記事で解説していきます!
![積分の基礎!積分とは何??[数学入門]](https://retu27.com/wp-content/uploads/rapture_20210422232830-383x500.jpg)
積分とは微分の逆操作!
今、関数f(x)とその導関数f'(x)があるとします。つまり、f(x)を微分するとf'(x)になるものとします。
このときに、積分は↓のような意味合いになります
積分=導関数f'(x)からf(x)を求める計算
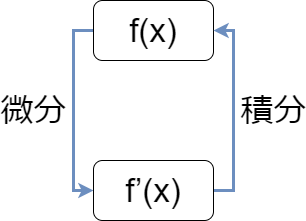
微分はf(x)から導関数f'(x)を求める計算です。積分は↓図のようにf'(x)からf(x)を求める計算になります。つまり微分の逆演算です!
 その逆で
その逆で
積分演算は↓のように\( \int\)という記号を用いて表します。積分をすると、導関数から元の関数f(x)に戻せるわけですね。ただ、ここについては微分とは違って制約があります。
\( \int f'(x) dx = f(x)\)
積分は完全に元の関数を推定出来ない!
上の説明では、積分によって導関数を元の関数に戻せるような説明をしましたが、実は少し違います。
導関数は、関数の傾きの変化をグラフ化したものです。ですので、導関数から、関数の動きを完璧に追うことができます。例えば、f(x)がx=0の地点からどれぐらい変化したかは計算可能なんです。
しかし、導関数には不足点があります。それは「f(x)がx=0の地点でどこから始まったのかが分からない」という事です。変化は分かるけど、初期点がわからない、、、そんな状況にあるんです!
なぜなら、↓の例のように微分すると定数は消えてしまうからです。微分は「変化」「傾き」を求める演算です。ですので変化の無い定数は消えてしまいます。
↓微分 定数は消える
\( f'(x) = 2x + 1 \)
だから、↓のように積分しても定数が何だったか推測できないんですね><
↓積分 定数は不明
\( f(x) = x^2 + x + ?? \)
ですので、実際の積分では不明となった定数をCとして↓のように表記します。Cは積分だけでは推定できない項です。
\(\int f'(x) = f(x) + C\)
この未定となる定数をCを積分定数といいます。
積分シミュレーター!積分のイメージを理解しよう!
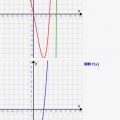
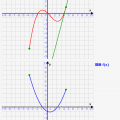
このシミュレーターでは導関数
の各パラメタa~cを変更すると、導関数グラフがそれに従って描かれます。また、その導関数からの推測で、元関数グラフを描いていきます。
導関数の値をもとに、傾きが求められ、元関数が復元される様子を確認しましょう!
また、積分定数Cを変えて見て、同じ積分でもグラフの位置が変わることを確認しましょう!
\( {f'(x)=} \) + 1\( {x^2 } \) + 1\( {x } \) + 1
\( {f(x)=} \) + 1\( {x^3 } \) + 1\( {x^2 } \) + 1\( {x } \)
↓値を変えると、自動的にアニメーションが始まります!
↑動的に再生速度を変えられます。左端で0にすると、一時停止となります。
まとめ:積分は微分とは逆演算だけど、クセがある><
最後にまとめです。今回は積分の基礎について解説しました。
積分は、微分とは逆演算で、「導関数f'(x)から元関数f(x)を推測する演算」です。しかし微分で定数項が消えてしまっているため、完全な推測はできないんです。
なので、積分定数Cという未確定な項がどうしても入ってしまうんです、、、><
次回はこの辺りを踏まえて、定積分と不定積分について詳しく解説します。
⇒「積分」カテゴリ記事一覧
その他関連カテゴリ