合成関数の微分の概念・イメージをシミュレーションで理解しよう![数学入門]
本記事では合成関数の微分について解説していきます。微分の基礎は、前回の記事でも説明しました。今回はその発展として、合成関数の場合にどのように微分するのかを解説します!
合成関数の微分は頻出する重大要素です。ただ公式を覚えるだけでなく、その意味やイメージを理解することがすごく重要なんです!
![合成関数の微分の概念・イメージをシミュレーションで理解しよう![数学入門]](https://retu27.com/wp-content/uploads/rapture_20210422204810-364x500.jpg)
目次
合成関数の微分公式
合成関数y=f(g(x))の微分について考える事にします。以後、f(x),g(x)ともに微分可能な関数という前提があるものとします。結論からいうと、合成関数の微分は↓のようになります。
$$ \large{ \{f(g(x))\}’=g'(x) \cdot f'(g(x)) }$$
これは2関数の合成関数があったら、g(x)とf(x)それぞれ別で微分して乗算すればよいことを示しています。
やや分かりにくいので別表現で示します。上の微分公式をdy,dtという記号で示したのが↓です。この表現では分かりやすくするためにt=g(x)と、中間変数tを用いて表現します。
\(t=g(x), y=f(t)とすると\)
$$ \large{ \frac{dy}{dx}= \frac{dy}{dt} \frac{dt}{dx} }$$
つまり、元の\(\frac{dy}{dx}\)は、t=g(x)をxで微分したもの(\(\frac{dt}{dx}\))とy=f(t)をtで微分したもの(\(\frac{dy}{dt}\))を乗算すれば良いといっているわけです。
以後、この公式の証明と図解・シミュレーターを用いた解説をしていきます。
合成関数の微分の例
上記の解説だけでは難解なので、1つだけ例を解説しておきます。
\(y = (x^2 + x)^2\)
このような複雑な関数でも
\( y=f(t) = t^2\)
\( t=g(x) = x^2 + x \)
と表現すると
\(= g'(x) \cdot f'(g(x)) \)
↓ g'(x)は普通に微分
\(= (2x + 1) \cdot f'(g(x)) \)
↓ f’(t)=2tであり、\(t=g(x)=(x^2 + x)\)のため…
\(= (2x + 1) \cdot 2(x^2 + x) \)
となります。\(f'(g(x))\)が複雑ですが、f(t)を微分して、そこにt=g(x)を代入するれば良いんですね!
一般的な「合成関数の微分」の証明方法
一般的な上記の合成関数の微分を証明する手順は↓の通りです。
↓f(x),g(x)の微分形式に近づける
\(\displaystyle = \lim_{ h \to 0 } \frac{f(g(x+h)) – f(g((x))}{g(x+h) – g(x)} \cdot \frac{g(x+h) – g(x)}{h} \)
↓ k = g(x+h) – g(x) ⇒ g(x+h)=g(x)+kとする
\(\displaystyle = \lim_{ h \to 0 } \frac{f(g(x)+k) – f(g(x))}{k} \cdot \frac{g(x+h) – g(x)}{h} \)
これを見ると後半の\(\frac{g(x+h) – g(x)}{h}\)は導関数g'(x)の定義そのものですね。前半部分はややこしいですが、t=g(x)とすると
\(\displaystyle = \lim_{ h \to 0 } \frac{f(t+k) – f(t)}{k} \)
\(\displaystyle = \lim_{ k \to 0 } \frac{f(t+k) – f(t)}{k} \)
とできます。なぜなら、hが0に収束するならばk= g(x+h) – g(x)も0に収束するからです。これは、g(x)は微分可能→連続という前提があるからです。連続なら、hが小さくするとkも小さく出来るはずなんです。
なので、hが微小量になると、g(x+h)とg(x)の値も近づくため、kも0に収束するはずなんです。そのため、前半部分は導関数f’となるわけです。
なので、結局、\(\{f(g(x))\}’=g'(x) \cdot f'(g(x))\)が証明できるわけです。ただし、微分する地点はxでなくt=g(x)の地点であることに注意して下さい。
合成関数の微分は、掛け算すればOK!そのイメージを理解しよう!
ここまで、合成関数の微分について解説してきましたが、証明だけではイメージが沸かないですよね。ということで、ここからはイメージ的な理解に向けての解説です。
そのために微分の意味を↓のように考えるようにしてみます。
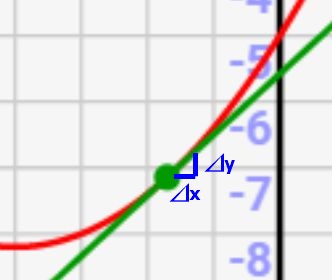
微分値=ある関数をx地点で微小量⊿xだけ増加させた時に、yが⊿xの何倍伸びるかを示す値
微分とは一点で定義される「接線の傾き」を求めるものですが、微小量の世界で考えると↑のような表現が可能です。つまり、関数がxのインプット地点で微増したとき、アウトプットyがその何倍で出力できるか、、、って値なんです。
絵にすると↓のような感じ。あまりに⊿xが大きいとズレますが十分に小さければ、このような考え方ができます。
すると、、、合成関数でも考え方は一緒です。インプットの微増⊿xに対して、最終アウトプットがその何倍になっているかを計算できればOKなんです。
そのため、例えば
入力t → f(t) → 出力y ⊿y=⊿tのβ倍
というように、g(x)でα倍、f(t)でβ倍されるとします。
すると、最終的なインとアウトの比率は
となり、αとβの乗算と言えるわけです!⊿xを十分に小さくすれば、結局\(α=g'(x),β=f'(t)\)のため、結果的に上記の証明と一致します。
このように、「微分値=インプットの微小量増加⊿xに対して、アウトプットの微小量増加⊿yは何倍か示す値」と考えると分かりやすいです!
「合成関数の微分」をシミュレーターで理解しよう!
上記のように長々と解説してきましたが、合成関数の微分は2つの微分値の掛け算で計算できるんです。
そのイメージを理解するためにシミュレーターを作ってみました!今回は↓のようなg(x),f(x)でシミュレーションします。
\(y = f(t) = t^2 -5 \)
↓のスライドバーで入力xを変化させて、g(x),f(t)の出力t,yがどのように変わるのか確認しましょう。また、g(x),f(t)の微分値の乗算が合成関数の微分値になることを確認しましょう!
合成関数の導関数を計算すると↓のようになります。これと結果が一致することも確認しましょう!
\)
*シミュレーターではg(x)の結果をt=**という形式で表示しています。これがf(t)のインプット値になっていることを確認しましょう
まとめ:合成関数の微分を使うと、微分が楽に!公式に当てはめるだけでなく、ちゃんとイメージを掴もう!
まとめです。合成関数の微分は上で示したように、↓の公式で求めることができます。
$$ \large{ \{f(g(x))\}’=g'(x) \cdot f'(g(x)) }$$
これはg(x)とf(x)の微分値を掛け算すれば、合成関数f(g(x))の微分値・導関数を計算できることを意味しています。
式に当てはめるだけだと何が何だか分からないですが、、、実際は↑のシミュレーターのように2つの関数に関係性があるんですね。そして、上で解説したように「微分値=インプットの微小量増加⊿xに対して、アウトプットの微小量増加⊿yは何倍か示す値」と考えると、非常に分かりやすくなります。
合成関数は数学でも物理でもよく出てくるものであり、ここでつまずくと理解が追いつかなくなるので、難しいですが必ず理解するようにしましょう!
⇒「微分の基礎」カテゴリ記事一覧
その他関連カテゴリ