物理入門:「斜面での垂直抗力」の基礎をシミュレーターで理解しよう!
目次
「垂直抗力(斜面)」をシミュレーターで確かめてみよう!
今回は基礎的な重力と垂直抗力の話をしました。平面では、重力とは同じ大きさの垂直抗力が物体にかかり、合力0でつりあっているという話でした。
しかし、斜面のときには垂直抗力と重力は同一になるとは限りません。今回は斜面での垂直抗力について考えていきます!
平面時の垂直抗力のおさらい
まずは前回のおさらいです。重力と垂直抗力は↓の式で表せます。
垂直抗力\(\displaystyle = mg \)
- m : 質量[\(kg\)]
- g : 重力加速度[\(m/s^2\)]
ポイントは垂直抗力N=重力となること。つまり、垂直抗力Nもmgとなります。
斜面時には、地面に対して垂直にかかる重力分だけ垂直抗力がかかる!
斜面での垂直抗力の考え方
それでは斜面時の垂直抗力について考えてみます。ポイントは「垂直抗力は、地面に対して垂直にかかる力に対しての反作用」ということです。
これを絵にしたのが↓です。斜面の時、垂直抗力はこのように斜めの力になります。垂直抗力自体が地面が垂直に反発する力なので、当たり前ですよね。
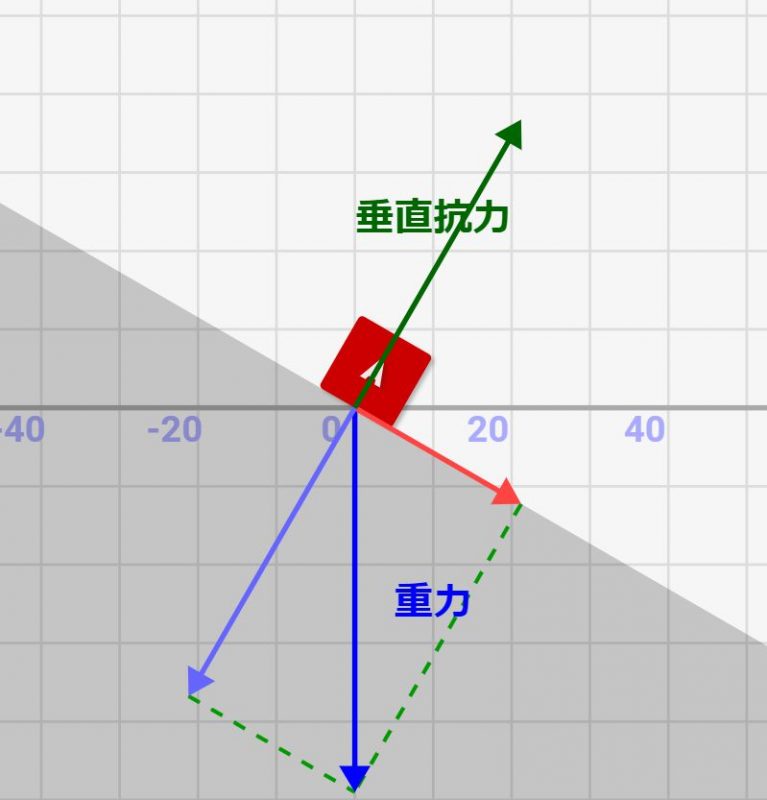
また、垂直抗力の大きさも、「地面に垂直にかかった力だけ」かかります。この力は、コチラの記事で解説した「力の分解」の考え方を用いれば計算できます。重力は下方向にかかりますが、これを地面に並行な方向の力(薄赤矢印)と、地面に垂直な方向の力(薄青矢印)に分けられるんです。
この分解した力の、薄青矢印の地面垂直分だけ垂直抗力として物体にかかる事になります。そして、地面へ移行の薄赤矢印は物体を地面に平行に移動させる力としてかかります(この部分は別記事で解説するので、今は無視します)
斜面での垂直抗力の公式
上記のように地面に対して垂直にかかる重力を求めます。今、地面が↓のように角度θで傾いているとします。すると、絵のように薄青矢印は重力と角度θをなすことがわかります。
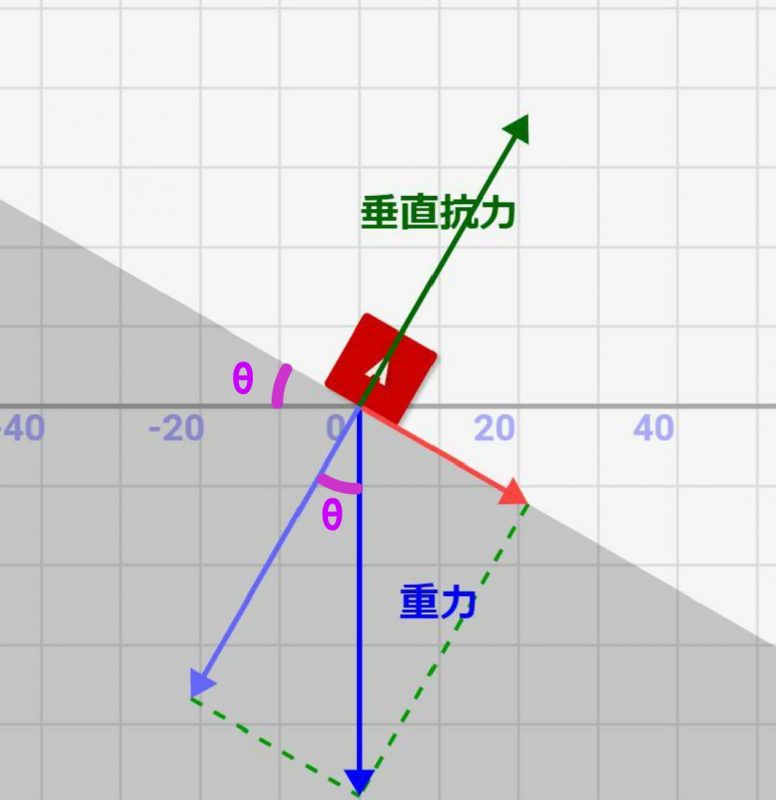
そのため、コチラの記事でも書いていますが、隣り合う線はcosθをかけることで変換できるので↓のように求めらます!
\(垂直抗力 \displaystyle= mg cosθ \)
- m : 質量[\(kg\)]
- g : 重力加速度[\(m/s^2\)]
- θ : 地面の傾斜度[度]
重力 ≠ 垂直抗力
重力・垂直抗力シミュレーター(斜面)
上記の通り、斜面では垂直抗力は、傾斜角度θとして、\(mg cosθ\)となります。これを実際にシミュレーターで確認してみましょう!
- ↓のスライドバーで物体の重さと、斜面の角度が変えられます
- 重力・垂直抗力の大きさが変わることを、実験して確認してみましょう
値を変えて、物体の動きを確かめましょう!
cosθ : 0.0
垂直抗力 : 0.0
物体は本当は落下する??
角度が90度に近づくと、ほとんど垂直抗力がかからないことがわかります。というより、実際はここまでいくと物体は落ちたり滑ったりしていきそうですよね!
上記のシミュレーターでは、地面に平行方向の赤矢印の影響を無視しています。本当はそちらの方向にモノが加速していって動いていくはずなんですよね。
ただ、常に動くとは限りません。物体が動くか動かないかは、静止摩擦力とその力との兼ね合いで決まります!詳細はコチラのページで!
- 斜面の場合は、斜面に垂直な方向の分だけ垂直抗力が発生する
- 斜面の角度がキツくなるほど、垂直抗力は小さくなっていく
⇒「重力・摩擦力」カテゴリ記事一覧
その他関連カテゴリ












