「単位ベクトル」をシミュレーション/図解で理解しよう![数学入門]
本ページでは数学のベクトルの基礎について、シミュレーターを用いてその意味・定義について解説しています。
今回は「単位ベクトル」についての解説です。前回、ベクトルのを実数k倍して自由に大きさを変えられることを説明しました。これを用いて、ベクトルを「大きさ」と「方向」に分離するときに便利なのがこの単位ベクトルです!
目次
単位ベクトルとは?
単位ベクトルは簡単にいうと、「方向を変えずに、強制的に大きさ1に変換したベクトル」です。その定義は以下の通りです。
\( \vec{a} \)ベクトルと同じ方向を持ち、大きさが1のベクトル
このようなベクトルを\( \vec{a} \)が作れます(零ベクトルの場合除く)。その数式定義は以下の通りです。
\( \vec{a}の単位ベクトルの求め方 \)
\( \displaystyle = \vec{e} \)
\( \displaystyle = \frac{\vec{a}}{|\vec{a}|} \)
\( \displaystyle = (\frac{x}{|a|},\frac{y}{|\vec{a}|}) \)
大きさを1にしたいので、元のベクトルの大きさ\(|\vec{a}|\)で割っています。こうすることで作られる\( \frac{\vec{a}}{|\vec{a}|} \)は大きさ1であり、実数倍してるだけなので方向は同じです。つまり、大きさ1で同じ方向となる単位ベクトルが作成できているわけです!
このようにして作成した単位ベクトルを通常\(\vec{e} \)という記号で表します。
元の大きさがない唯一のベクトル=零ベクトルだけは、単位ベクトルを作れないことに注意して下さい!
単位ベクトルは半径1の円/球上にある
これも自明なことですが、単位ベクトルは必ず半径1の円(2次元)/球(3次元)上にあります。長さ1なので当たり前ですね!もっというと、「全ての方向の単位ベクトルを集めると、↓のような円/球になる」ともいえるわけです。

単位ベクトルを使うと、ベクトルを「大きさ」と「方向」に分けて表現できる!
単位ベクトルは純粋に方向を示すために定義されたものです。これを使うと、様々なベクトルを「大きさ」と「方向」に分けた形で表現可能です。
\( \vec{a} \)
\( \displaystyle = |\vec{a}| * \vec{e} \)
↑の\(|\vec{a}|\)がベクトルの大きさを、\(\vec{e}\)がベクトルの方向を表しています。この表現だと、このベクトルの大きさがどれぐらいで、どの方向を向いているかが一目で分かって便利なのです!
シミュレーションでベクトルの大きさを理解しよう!
単位ベクトルをイメージで理解するため、シミュレーターを用意しました!元ベクトルの各成分を変えられるので、色んなパターンの単位ベクトルを確認してみましょう!
2次元ベクトル シミュレーター
まずは簡単に2次元の例からです!
- x,y成分を変更すると、青矢印のベクトルが動きます
- そこから計算した単位ベクトルを赤矢印で表示します
- 必ず緑色で示した単位円上に単位ベクトルがのることを確認しましょう
↓値を変えると、ベクトルを変動できます
\(\vec{e} =\)
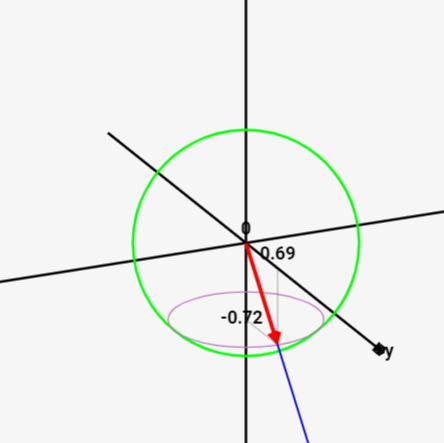
3次元ベクトル シミュレーター
次に3次元の例です!
- x,y,z成分を変更すると、青矢印のベクトルが3D空間で表示されます
- そこから計算した単位ベクトルを赤矢印で表示します
- 単位ベクトルと緑色の球との接面を紫色で表示してます
- 単位ベクトルが球の上にのっていることを確認してみましょう
↓値を変更して、単位ベクトルが球上につくられることを確認しましょう!
\(\vec{e} =\)
↓表示角度(上下)をコチラのバーで調整可能です!
まとめ:単位ベクトルを使うと「大きさ」と「方向」を分離できる!
最後にまとめです。単位ベクトルは、その大きさが1のベクトルです。これは、各ベクトルをその大きさで割ることで作る事ができます。方向は元ベクトルと同じです。単位ベクトルを使うと、↓のようにベクトルを「大きさ」と「方向」に明確に分離した表現に置き換える事ができるんです!とても便利です。
\( \vec{a} \)
\( \displaystyle = |\vec{a}| * \vec{e} \)
また、シミュレーターで確認した通り、単位ベクトルは円・球上に必ずのることが重要な性質となります!
次回はベクトルの足し算について解説します!
⇒「ベクトル」カテゴリ記事一覧
その他関連カテゴリ