組み合わせの考え応用!最短経路選択問題をシミュレーターで理解しよう![数学入門]
この記事では、組み合わせパターンのまとめとして「経路選択問題」を考えてみます。
この経路選択問題をシミュレーターを用いて考え、組み合わせとは何かを復習していきたいと思います!
![組み合わせの考え応用!最短経路選択問題をシミュレーターで理解しよう![数学入門]](https://retu27.com/wp-content/uploads/rapture_20200623224643-500x472.jpg)
目次
復習:組み合わせ問題は「n個のクジから、r個選ぶ」ときのパターン総数を考えること
前回までの記事で、順列と組み合わせの考え方について解説してきました。まず、順列というのは「n個のクジから、r個引く」時のパターンを考える問題であり、そのパターン数は以下のようになります(詳細はコチラの記事へ)
\( {}_n P_r = n \cdot (n-1) \cdot … \cdot (n – r + 1) \)
これに対して組み合わせとは「n個のクジから、r個選ぶ」時のパターンを考えることです。似ていますが、違います。r個選ぶ、なので引いたものの順番は関係ないんです。
そしてその組み合わせのパターン数は以下のようになります(詳細はコチラの記事へ)
\( \displaystyle {}_n C_r = \frac{n \cdot (n-1) \cdot … \cdot (n – r + 1)}{ r! } \)
簡単にいうと、「順列」は引いたクジの順番を区別しますが、「組み合わせ」はそれを意識しません。引いたr個のクジは、パターン数r!だけ重複があるのです。その分を\({}_n P_r\)から割り引いたのが\({}_n C_r\)になります。
組み合わせの考えを応用して、経路選択問題を考えよう!
問題設定
それでは組み合わせの考えを応用して、経路選択問題を解いてみましょう。
経路選択問題とは、↓のような経路があるときに最短経路でSTARTからGOALにたどり着く経路が何パターンあるかという問題です。
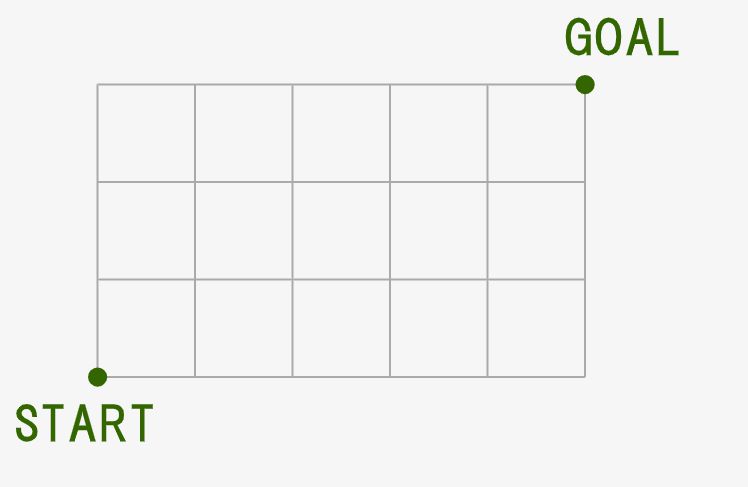
↓がその経路の一例です。「上向き移動」と「右移動」を組み合わせてGOALに最短でたどり着いています。

考え方
まず、上記のような最短経路となる条件は「右と上の移動だけで進むこと」と言えます。左あるいは下にいくので、右と上への移動だけでたどり着くのが条件になります。
そして、上の例では縦方向に3マス、横方向に5マスあるので、「上方向に3回、右方向に5回移動する」ことが必要になります。合計8回移動するわけですね。
こう考えていくと、、、実は「この経路パターンを考えること = 組み合わせ問題を考えること」と見なせるのです。この経路パターンは「合計8回の移動の中で、上方向への移動3回をいつ行うか」という問題です。そのため「上へいつ移動するかをクジ引きで選択」すると考えます。例えば、クジを引いて1,3,5が出たら、↓のように1回目、3回目、5回目で上に移動することにします。
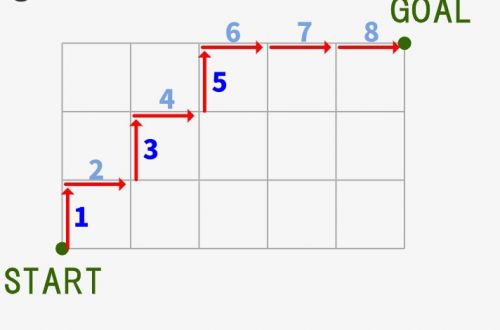
すると、上記の問題は「8個のクジの中で、3つのクジを引くのは何パターンあるか」と読み替えることができます。クジによって、経路が1対1に決まるためです。「引いたクジの番号のとき上移動」「余ったクジの番号のとき右移動」すると決めれば、「このクジ引きのパターン数=経路のパターン総数」となるのです!
シミュレーターで経路選択問題と組み合わせパターンを理解しよう!
経路選択問題をシミュレーションできるツールを作成しました。
- スライドバーで横マスと縦マス数を変更すると、実行開始します
- シミュレーターは上記解説の考えの通り、クジ引きをして経路パターンを決めます
- 組み合わせの考えをもとに、全てのパターンを列挙していきます
色々値を変えて、実験してみましょう!
…
↓数字はクジを引いた結果を表しており、青い部分が前回クジから変わった部分を示しています。
↓このスライドバーの値を変えると、シミュレーターを高速に実行できます。パターン数が多い場合は最高速度で動かすこと推奨です!
まとめ:組み合わせパターンを考える問題は色んなところで出てきます!
最後にまとめです。今回の最短経路選択パターンを考える場合では、うまく考え方をかえることで、実はクジ引きでの組み合わせパターン問題に置き換えられます。
このように、一見すると全くクジとは関係ないような問題が、実は組み合わせを考える問題と同値であったりします。(実は、式のたすき掛けもこの組み合わせ問題に絡んでいたり…その話は別記事で解説予定です)
このような順列/組み合わせを考えることは非常に重要です。現実の問題でも、組み合わせの考えが必要になること多くなるので、階乗、P記号、C記号の概念を理解しておきましょう!
- 経路問題は、実はくじ引き問題を形を変えたもの。クジ引きとの公式を使えば解ける
⇒「順列/組み合わせ」カテゴリ記事一覧
その他関連カテゴリ














