等差数列をシミュレーション/図解で理解！[数学入門]

2021-02-24　

本記事では数学の「等差数列」について詳しく説明していきます。まず数列とは、「数が順番にならんだもの」を意味します。例として「1,7,5,3,12」「3,6,9,2,11」などが挙げられます。そして等差数列とは、その中でも「隣同士の数の差が同じもの」の事を言います。

1 等差数列とは
- 1.1 等差数列の用語
- 1.2 その他の等差数列の例
2 等差数列の一般表記
3 等差数列をシミュレーションで理解しよう！
4 等差数列の和を計算してみる！難しいようで、意外と簡単です！
5 等差数列の和の計算を、シミュレーターで理解しよう！

等差数列とは

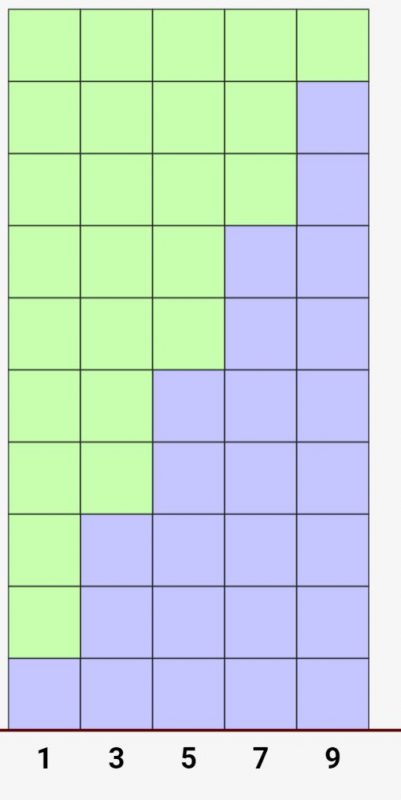
例えば↓が等差数列の例です。この数列は1ずつ値が増えていっていますよね。つまり隣同士の値の差は常に1。なのでこれは等差数列と言えます！

\( 2,3,4,5,6 \)

↓図で表すとこんな感じ。等差数列は差が同じなので綺麗な階段状になります。

　

POINT等差数列は前後の差が同じで、階段状になる数列！

等差数列の用語

ここで等差数列を表す時に必要な用語の説明をします。

初項：数列の最初の項

交差：隣同士の数の差

項数：項が何個あるか

初項は最初の数を意味します。つまり、一番左側の数ですね。そして交差は各数の差です。つまり上の例は、初項が2で交差が1の等差数列と言えます。
大事なのは、等差数列はこの2つが決まれば全ての項が表せるということです。最初の数と、それ以後の数の差がわかれば、以後の数が全て決まりますから。

その他の等差数列の例

別の等差数列の例を説明します。

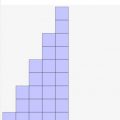
↓コチラも同じく等差数列になります。5,7,9と2ずつ増えていっているので交差は2になります。初項は見ての通り5ですね。

[例1]
\( 5,7,9,11,13 \)

↓図はこんな感じ。2ずつ増えていってます。

　
　
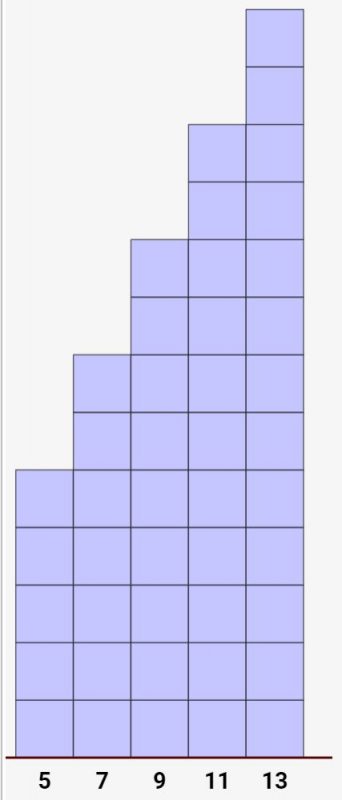
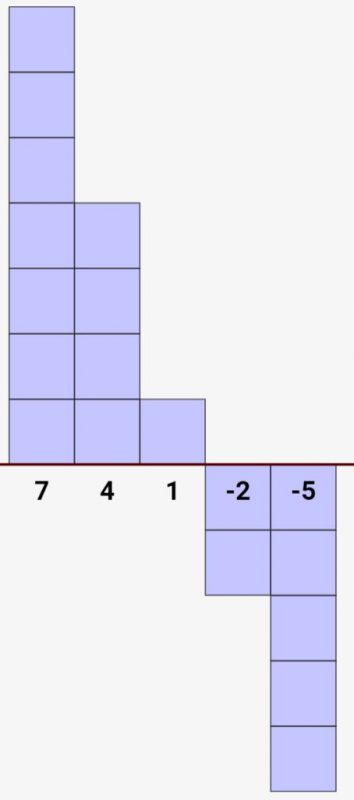
↓コチラは上記の例とは違いますが、同じく等差数列です。7,4,1と3ずつ下がっていますね。なので、交差は-3になります。見ての通り、初項は7です。

[例2]
\( 7,4,1,-2,-5 \)

↓交差-3なので、下がっていくイメージ。マイナスにも突入します

等差数列の一般表記

上でいくつか例に挙げた等差数列は以下の表記で定義できます。

\( a_n = a_1 + (n – 1) \cdot d \)
* \(a_1\): 初項
　\(d\): 交差(各項の差分）

等差数列は初項と交差(各項の差分）をn-1個足すことで各項を計算できるというわけです。各nで値を当てはめてみると分かりやすいです。1つ目は\(a_1\)で、2つ目は\(a_1 + d\)、3つ目が\(a_1 + 2d\)と表せます。\(a_1\)から始まり、\(d\)がその後一つずつたされていくわけです！

等差数列をシミュレーションで理解しよう！

今まで説明した等差数列をさらにイメージしやすくするため、シミュレーターを用いて自分で値を指定して等差数列を確かめてみましょう！

シミュレーターの説明

初項(\(a_1\))、交差(\(d\))、項数(\(n\))を指定すると、数列をブロック形式で図示してくれます
値を変えると再描画するので、色々値を変えてイメージを掴みましょう

初項

交差

項数

等差数列の和を計算してみる！難しいようで、意外と簡単です！

「シミュレーターで作った等差数列」を全ての数字を足すといくつになるでしょうか？ブロックを一つ一つ数えても良いですが、もっと一般化した計算方法があります。
　
どうやって計算するか難しそうですが、、、実はイメージさえつかめば簡単なんです。↓の青色ブロックが求めたい等差数列の和です。とすると、実は同じブロックを逆向きに足せば(緑ブロックで示してます)、長方形になるんです！

この長方形は「横 = 項数n」「縦 = 初項\(a_1\)と最終項\( a_n\)の和」になります。この長方形の面積の半分が求める総和になりますので、

等差数列の総和
↓長方形の面積/2
\(= \displaystyle \frac{ n \cdot (a_1+a_n)}{2} \)
↓\(a_n\)を初項と交差を使った形に変換
\(= \displaystyle \frac{ n \cdot (a_1+\CB{a_1+d(n-1)})}{2} \)
\(= \displaystyle \frac{n}{2}(2{a_1}+d(n-1)) \)

という形で計算できます。

項にマイナスが現れた時も同じ式で計算できます。 全ての項がマイナスの場合もこんな感じでマイナスブロックを総和すればOKです。
　
項にプラスとマイナスの項が出たときはややこしいので↓の等差数列の総和シミュレーターでイメージを掴んでください！
　

POINT等差数列の合計は、2つ組み合わせれば長方形の面積として求められる！