分子運動シミュレーターで圧力・温度の本質を理解しよう!(多分子の圧力編)![物理入門]
前回の記事で、1つの分子が片側の壁にもたらす力Fを求める過程を、シミュレーターを用いて確認しました。
今回は、その発展で、多くの分子を用いるたとき、どの程度の圧力かかるかを求めていきます!
![分子運動シミュレーターで圧力・温度の本質を理解しよう!(多分子の圧力編)![物理入門]](https://retu27.com/wp-content/uploads/rapture_20210505183258-500x330.jpg)
目次
シミュレーターで分子1000個でかかる力Fを観察しよう!
さっそくですが、シミュレーターで実験です。シミュレーターで1000分子の動きを観察してみましょう!「薄青で塗った壁にどれだけの力Fを平均して与えるか」を考察するのが今回のテーマです。
- \(10m^3\)の立方体の箱で分子が動くことを想定
- 分子は初期位置と角度がランダムで配置されます
- 分子は簡単のため質量m=0.01とする
- x,y,z方向の壁では反発係数1でエネルギーの消失なく反発する
- 分子が壁にぶつかると0.1秒で壁に一定の力を与えて跳ね返る
- スライドバーで分子の速度\(v\)を指定可能です
- 薄青壁に分子がぶつかると、青く光ります
- 下のグラフは横軸に時間t、縦軸に薄青壁が受けた力を図示しています
- 速度が速いので、初期値で再生速度0.5にしています(2秒かけて1秒の動作を再生します)
↓スライドバーで分子の速度vを変更して、どのように力が働くか実験してみましょう!
↑動的に再生速度を変えられます。左端で0にすると、一時停止となります。
↓横軸=時間t、縦軸=片側壁が受ける力F
このシミュレーターの結果を以下考察していきます。
前回のおさらい
まずは前回のおさらいです。上のシミュレーターでは一変を10m、物体の重さを0.01kgとしましたが、定式化して考察するため↓のように記号化して考察します。
分子の重さ:m
分子の数:N
分子のx軸方向の速度:\(v_x\)
分子の速度: v
前回考察したとおり、1分子が片側の壁に与える力Fは↓の式で求められます。
\( \displaystyle \frac{m{v_x}^2}{L} \)
これを用いて、大量の分子が与える力を求めていきましょう!
大量の分子が壁に与える力と圧力を求める!
x方向の速度vに変換する
まずは速度についての論議が必要です。↑の式で使われているのはx方向の速度\(v_x\)ですが、一般的に想定したいのは分子自体の速度vです。この2つには↓のような関係性があります(三平方の定理の3次元版)
ですが、現在考えているのは膨大な分子がある場合で、ランダムに分子が飛び交っている状況です。この場合、x方向、y方向、z方向で速度の偏りがないはずという仮定ができます。具体的にいうと↓の仮定です。つまり、全ての方向で同じ速度という仮定です。
\( {v_x}^2 = {v_y}^2 = {v_z}^2 \)
こうした場合、↑の式を変形すると
↓変形
\( \displaystyle {v_x}^2 = \frac{v^2}{3} \)
と導けます。つまり、x方向の速度の二乗は、分子の速度自体の二乗の1/3とみなせるのです!
分子N個での力と圧力を求める!
ここまでくれば簡単です。あとはN個の分子を足し合わせるだけです。1分子あたりの力Fは↓なので、
\( \displaystyle \frac{m{v_x}^2}{L} \)
これの\(v_x\)をvとして、N倍にすればいいだけです。
\( \displaystyle \frac{N × m{v_x}^2}{L} \)
↓ \(v_x\)をvに入れ替え
\( = \displaystyle \frac{N m{v}^2}{3L} \)
これが片側の壁にかかる力Fです。圧力は、コチラのページで解説したように、力Fを面積Sで割ればよいだけです。今、全ての辺がLなので、面積は\(L^2\)です。なので、、
\( 圧力P \displaystyle = \frac{N m{v}^2}{3L} × \frac{1}{L^2} \)
\( \displaystyle = \frac{N m{v}^2}{3L^3} \)
↓\(L^3\)は体積Vに変換可能
\( \displaystyle = \frac{N m{v}^2}{3V} \)
となります。\(L^3=V\)と体積に置き換えました。これで、体積Vと圧力Pが反比例する事実が明らかになりましたね!
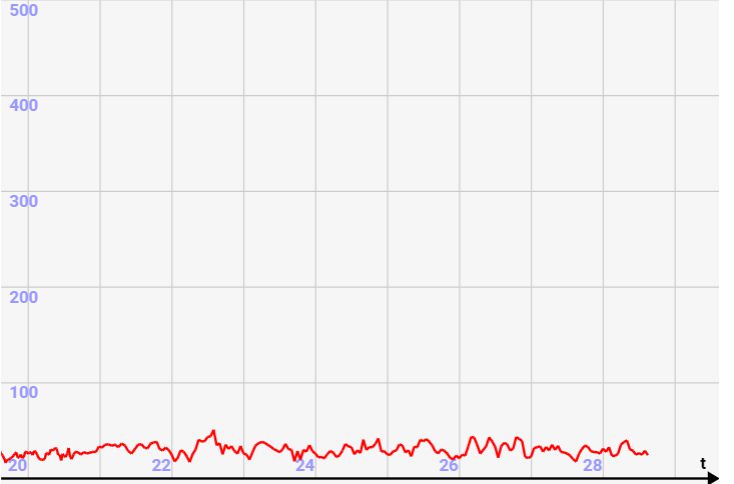
ちなみに、上記のシミュレーターではm=0.01,N=1000,V=1000なので、↓のような圧力になります。v=10の場合はF=100/3,P=1/3となります。この結果と一致しそうか確認してみましょう!
↓v=10の時のFのグラフ。大体、F=33辺りで変動しているのが分かりますよね!
最後に分子数Nをモル数nに置き換える
最後に分子数N(個)のままでは扱いにくいので、モル数nに置き換えましょう。変換は↓の式で可能です。
* N_A= \(6.02×10^23\) アボガドロ定数
すると↓の公式が出来上がります!
\( P\displaystyle = \frac{N m{v}^2}{3V} \)
\( =\displaystyle = \frac{n N_A m{v}^2}{3V} \)
まとめ:1分子の力をあわせていくと、全体の圧力Pが求められる!
今回のシミュレーターでは1000個の分子を使った実験をしてみました。この結果から、圧力Pが↓の式で求められることを導きました。
\( P=\displaystyle = \frac{n N_A m{v}^2}{3V} \)
この式が表すように、圧力は分子モル数nに比例し、分子速度の二乗に比例し、体積Vと反比例をなします。
これって、状態方程式PV=nRTに似ていますよね、、!ということで次回はこの関係から、絶対温度Tの正体を解き明かして行きます!
- 大量の分子がランダムで運動すると、数の論理により壁には均一的な力Fが働くようになる
- 力Fを面積Sで割ると、体積Vと圧力Pの関係性が見えてくる
⇒「分子運動と熱力学」カテゴリ記事一覧
その他関連カテゴリ











