物理入門:「水平投射」をシミュレーターで理解しよう!
前回までの記事で解説した等加速度運動の例として、「水平投射」をシミュレーターで動かしてみましょう!
地球にあるものには重力加速度g=9.8m/s^2が下方向に働いています。この重力により、ボールがどのような速度で落ちていくか、シミュレーターを用いて確認してみましょう!
水平投射シミュレーター
さっそくシミュレーターで実験してみましょう!
- 実行ボタンを押すと、初速x(\(v_0\))でボールが投げ出されます
- スライドバーで初期y(投げ出す位置)を自由に変えられます
- グラフ表示項目を選択すると、x,yそれぞれの位置/速度/加速度をリアルタイムにグラフ化して表示します
色々な高さから水平投射させて、実験してみましょう!
飛距離 : 0.0 m
グラフ表示項目位置
速度
加速度
xを赤色,yを赤色で示しています
シミュレーター結果解説
以下、シミュレーターの結果を解説していきます。基本的に、落下運動は加速度運動ですので公式に当てはめれば速度/位置等が求められます。
この時のコツはx方向(横)とy方向(縦)成分に完全に分けて計算するということです。
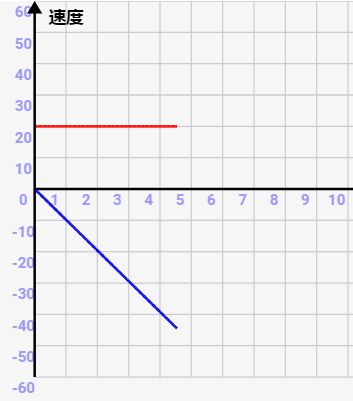
速度の変化
x方向とy方向で分けて考えます。
y方向の速度
下方向の速度は、等加速度運動なので↓のように時間に比例して大きくなっていきます。加速度は重力加速度-gになります。
\(v_y \displaystyle= -gt \)
- \(t\) : 時間[\(s\)]
- \(g\) : 重力加速度[\(m/s^2\)]
x方向の速度
x方向には何も力がかかりません。ですので、x方向は↓のように初速から変わらず、等速運動していきます。現実的には、永遠に速度が変わらないなんてなさそうですが、空気抵抗・摩擦がなければこのようになります。
\(v_x \displaystyle= v_0 \)
- \(v_0\) : 初期速度[\(m/s\)]
↓x方向を赤字、y方向を青字で示した速度変化です。y方向は直線的に大きくなっていきますが、x方向は一定の速度になります。
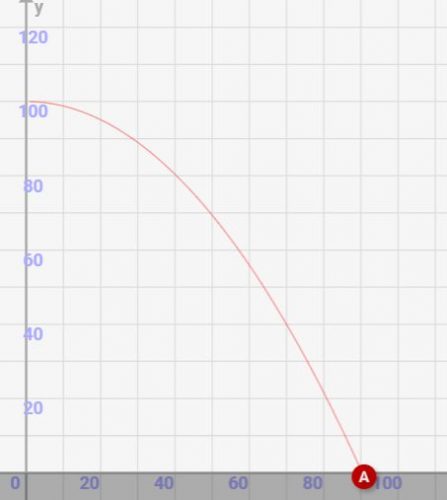
位置の変化
y方向の位置
水平投射時の位置は、等加速度の位置公式から↓のように求められます。
\(y \displaystyle= y_0 – \frac{1}{2}gt^2 \)
- \(y_0\) : 初期位置[\(m\)]
- \(t\) : 時間[\(s\)]
- \(g\) : 重力加速度[\(m/s^2\)]
つまり、水平投射ではボールの位置は↓のように二次関数状に変化します。
x方向の位置
x方向は等速運動なので、↓のようになります。簡単ですね。
\(x \displaystyle= v_0 t \)
- \(v_0\) : 初期速度[\(m/s\)]
- \(t\) : 時間[\(s\)]
↓結果的に、x方向とy方向は↓のような変化になります。xは直線的に増加していき、yは二次曲線のように0に向かっていきます。

地面到達時間
地面到達時間は↑の式にy=0を代入すれば簡単に求められます。これは自由落下運動と同様です。
\( t \displaystyle= \sqrt{\frac{2y_0}{g}} \)
- \(y_0\) : 初期位置[\(m\)]
- \(g\) : 重力加速度[\(m/s^2\)]
つまり、ボールを投げおろす\(y_0\)に対して、落ちるまでにかかる時間tはそのルートに比例して大きくなるわけです。
(高さが4倍になっても、かかる時間は2倍)
到達位置(x方向)
x方向の到達位置を求めるのは簡単です。地面への到達時間は↑のように求まっているので、これをx方向の位置「\(x= vt\)」の式に代入すればいいだけです。
\(x \displaystyle = v_0 t \)
\( \displaystyle = v_0 \sqrt{\frac{2y_0}{g}} \)
- \(v_0\) : 初期速度[\(m/s\)]
- \(y_0\) : 初期位置[\(m\)]
- \(g\) : 重力加速度[\(m/s^2\)]
シミュレーターで高さや初速を変えて実験してみて、このような到達位置になることを確かめてみて下さい!
- 水平当社は、鉛直方向は自由落下と全く同じ動きをする
- それ故に地面到着時間も自由落下と全く同じ
- 水平方向は単純な等速運動となる
⇒「重力・落下運動」カテゴリ記事一覧
その他関連カテゴリ














