物理入門:「自由落下」をシミュレーターで理解しよう!
前回までの記事で解説した等加速度運動の例として、「自由落下運動」をシミュレーターで動かしてみましょう!
地球にあるものには重力加速度g=9.8m/s^2が下方向に働いています。この重力により、ボールがどのような速度で落ちていくか、シミュレーターを用いて確認してみましょう!
自由落下シミュレーター
自由落下運動の動きをシミュレーターで確認してみましょう!
操作方法
- 実行ボタンを押すと、表示位置からボールが自由落下していきます
- スライドバーで初期y(ボールの高さ)を変えられます
- グラフ表示項目を選択すると、x,yそれぞれの位置/速度/加速度をリアルタイムにグラフ化して表示します
どのような運動になるか観察してみましょう!
経過時間 : 0.0 秒
グラフ表示項目位置
速度
加速度
xを赤色,yを赤色で示しています
シミュレーター結果解説
以下、シミュレーターの結果を解説していきます。基本的に、落下運動は等加速度運動ですので、公式に当てはめれば速度/位置等が求められます。
速度の変化
下方向の速度は、等加速度運動なので↓のように時間に比例して大きくなっていきます。加速度は重力加速度-gになります。
重力は高さyとは逆方向にかかるので、-gの加速度になることに注意して下さい。
等加速度運動の速度
\(v \displaystyle= -gt \)
- \(t\) : 時間[\(s\)]
- \(g\) : 重力加速度[\(m/s^2\)]
POINT自由落下では、鉛直方向の速度が時間に比例して増加していく!
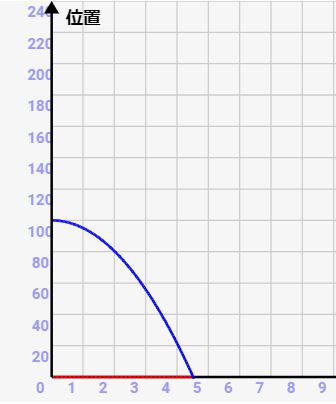
位置の変化
自由落下時の位置は、等加速度の位置公式から↓のように求められます。
等速運動時の位置
\(y \displaystyle= y_0 \ – \ \frac{1}{2}gt^2 \)
- \(y_0\) : 初期位置[\(m\)]
- \(t\) : 時間[\(s\)]
- \(g\) : 重力加速度[\(m/s^2\)]
つまり、自由落下ではボールの位置は↓のように二次関数状に変化するんですね。

地面到達時間
地面到達時間は↑の式にy=0を代入すれば簡単に求められます。
\( 0 \displaystyle= y_0 \ – \ \frac{1}{2}gt^2 \)
\( t \displaystyle= \sqrt{\frac{2y_0}{g}} \)
\( t \displaystyle= \sqrt{\frac{2y_0}{g}} \)
つまり、ボールを投げおろす\(y_0\)に対して、落ちるまでにかかる時間tはそのルートに比例して大きくなるわけです。
時間が経つほどボールは加速するので、かかる時間はそこまで伸びないんですね!(高さが4倍になっても、かかる時間は2倍)
シミュレーターで高さを変えて実験して、かかる時間がこの通りになることを確かめてみて下さい!
まとめ
- 自由落下では鉛直方向の速度が時間に比例して増加していく
- 落下までにかかる時間は高さのルートに比例する
⇒「重力・落下運動」カテゴリ記事一覧
その他関連カテゴリ















