置換積分法をシミュレーターで分かりやすく理解しよう!(合成関数の視点) [数学入門]
前回の記事までで、積分の別の見方について解説しました。
今回はその考え方を使って、積分の「面積計算」という視点で見てきます!
![置換積分法をシミュレーターで分かりやすく理解しよう!(合成関数の視点) [数学入門]](https://retu27.com/wp-content/uploads/rapture_20210509231752-1-360x500.jpg)
目次
置換積分の定義と例
まず置換積分の定義から示します。
置換積分の公式
置換積分にも不定積分と、定積分の2種類があります。
\( x=g(t)と置換したとき、\)
\( \displaystyle \int f(x) dx = \int f(x)\frac{dx}{dt} dt \)
\( \displaystyle = \int f(g(t))g'(t) dt \)
\( x=g(t)と置換したとき、\alpha=g({\alpha}’), \beta=g({\beta}’)とすると、 \)
\( \displaystyle \int_{\alpha}^{\beta} f(x) dx = \int_{{\alpha}’}^{{\beta}’} f(x)\frac{dx}{dt} dt \)
\( \displaystyle = \int_{{\alpha}’}^{{\beta}’} f(g(t))g'(t) dt \)
これは、考えようとしてるy=f(x)に対して、x=g(t)という置換を行う場合、↑のように変換すれば変数tの積分問題に変換できるというものです。
置換積分の例題
上の公式だけだと分かりにくいので例題として↓を積分してみます
\( \int_{-2}^{4} (2x – 3)^2 dx \)
今回はカッコの中の「2x – 3 = t」とすると、↓のように各関数を表せます。
\( \displaystyle x = \frac{t +3}{2} \)
↓x関数をtで微分
\( \displaystyle \frac{dx}{dt} = \frac{1}{2} \)
ここで定積分の上限下限は↓となるので、
\( x = 4 ⇒ t = 4*2 -3 = 5\)
最終的に↓のように問題を置き換えることができるんです!
\( \displaystyle \int_{-2}^{4} (2x – 3)^2 dx \)
↓ 2x -3 = tで置換
\( \displaystyle \int_{-7}^{5} t^2 * \frac{1}{2} dt \)
実際に計算すると↓のようになり、変換前/変換後が同値になることが分かります!
\( F(x) = \int (2x – 3)^2 dx = \frac{(2x -3)^3}{6} + C \)
\( 解 = F(4) – F(-2) = \frac{5^3}{6} – \frac{{-7}^3}{6} \)
[t変数で変換後]
\( F(t) = \int t^2 * \frac{1}{2} dt = \frac{t^3}{6} + C\)
\( 解 = F(5) – F(-7) = \frac{5^3}{6} – \frac{{-7}^3}{6} \)
置換積分の一般的な証明
置換積分の公式は↓の合成関数の微分の公式を使って証明できます。
\(x=g(t), y=f(x)とすると\)
$$ \large{ \frac{dy}{dt}= \frac{dy}{dx} \frac{dx}{dt} }$$
今、原始関数F(x)をtで微分することを考えます。↑の公式を使うと、
↓合成関数の微分公式
\( = \displaystyle \frac{d F(x)}{dx} \frac{dx}{dt} \)
↓F(x)の導関数はf(x)
\( = \displaystyle f(x) \frac{dx}{dt} \)
となります。この両辺を変数tで積分すると、、
↓左辺は導関数の逆演算
\( \displaystyle F(x) = \int f(x) \frac{dx}{dt} dt\)
↓x=g(t)
\( \displaystyle F(x) = \int f(g(t)) \frac{dx}{dt} dt\)
F(x)はf(x)をxで積分した関数なので、結局↓の置換積分公式が成り立ちます。ただし、↑の例のように積分範囲はx=g(t)の関係によって変わります。
\( \displaystyle \int f(x) dt = \int f(g(t)) \frac{dx}{dt} dt \)
…という証明の流れなんですが、いまいちイメージしにくいですよね。合成関数の微分を使っているのはわかるのですが。なぜ急に\(\frac{dx}{dt}\)が乗算されるのか、なぜ積分すべき範囲(α~β)が変わるのか、よく分からないですよね。
このあたりが明確になるように、シミュレーターを用いて解説していきます!
合成関数の積分のイメージ
置換積分とは合成関数の積分
↑のような置換積分の公式がありますが、重要なのは「合成関数をどうやって積分するか」のイメージです。ということで、以後、「合成関数の積分」という目線で解説していきます!
合成関数の微分のイメージのおさらい
上記の置換積分の公式に紐付いているのは合成関数の微分の概念です。なので、合成関数の微分の記事と同様、微小量⊿xを使って考えると非常に分かりやすくなります!
合成関数の微分のおさらいします。そもそも微分とは、y=f(x)という関数に対して、入力xを微小量⊿x上げた時に、出力yがどれぐらい変化するか(⊿y)を計算し、その比率\(\frac{⊿y}{⊿x}\)を求める演算です。
図にすると↓のような感じです。この⊿xに対して、⊿yが何倍か求めるのが微分のわかりやすいイメージです。
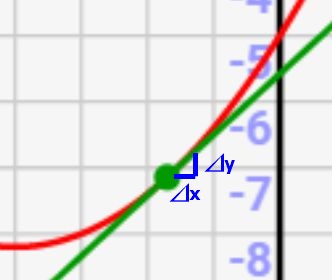
これに対して合成関数では、x=g(t)でα倍,y=f(x)でβ倍されると考えると、↓のように定式化できます。
\( \displaystyle 入力x → f(x) → 出力y ⊿y=⊿x \cdot β\)
このような関係の時、最終的な合成関数の入力・出力比率\(\frac{⊿y}{⊿t}\)は↓のように求められます。g(t)でα倍、f(x)でβ倍になるので、最終的に\(α \cdot β\)倍になります。\(α=\frac{dx}{dt},β=\frac{dy}{dx}\)なので、結局、合成関数の微分値は両関数の傾きの積になるんですね!このように微小量⊿で考えると、合成関数の微分値は当たり前のことを言っているんです。具体的なイメージはコチラのシミュレーターで確認頂けると、分かりやすいです!
合成関数の積分のイメージ
上の合成関数の微分の「二段階で変換する」という考え方を用いて、合成関数の積分も考えてみます。
積分のイメージを考える時に重要なのが、「lim Σf(x)*⊿x」のイメージです。これはコチラの記事で解説しています。この考え方でいうと、積分は「入力xを細かい⊿xに分割し、導関数f(x)の値と積をとって足し合わせていく」ことになります。なぜなら、↓の近似が成り立つからです。
F(x+⊿x) – F(x) ≒ f(x)*⊿x
そして、上記の論議の通り、⊿xは↓のように置き換えられるんです。g'(t)はx=g(t)関数の接線の傾きになります。
すると、上記式は↓のようになります。
F(x+⊿x) – F(x) ≒ f(x)*⊿x = f(x)*g'(t)*⊿t = f(g(t))*g'(t)*⊿t
以前の記事と同様に、これを無限に細かい⊿tにして足し合わせていけばOKです。最終的には↓のようになります。これは上記の定積分での変換と同じになります。
\( \displaystyle \int_α^β f(x) dx\)
\( \displaystyle = \lim_{ ⊿x \to 0 } \sum_{t=α’}^{β’} f(g(t))*g'(t)*⊿t\)
普通の積分との違いは「⊿x=g'(t)⊿tと変換して、t観点から積分を行うこと」だけです。つまり、\(\frac{dx}{dt}=g'(t)\)とはt観点からx観点へ変換するための、変換比率みたいなものなんです。
合成関数の積分の図的なイメージ
合成関数の積分を、実際にグラフで描いた例を見てみましょう。
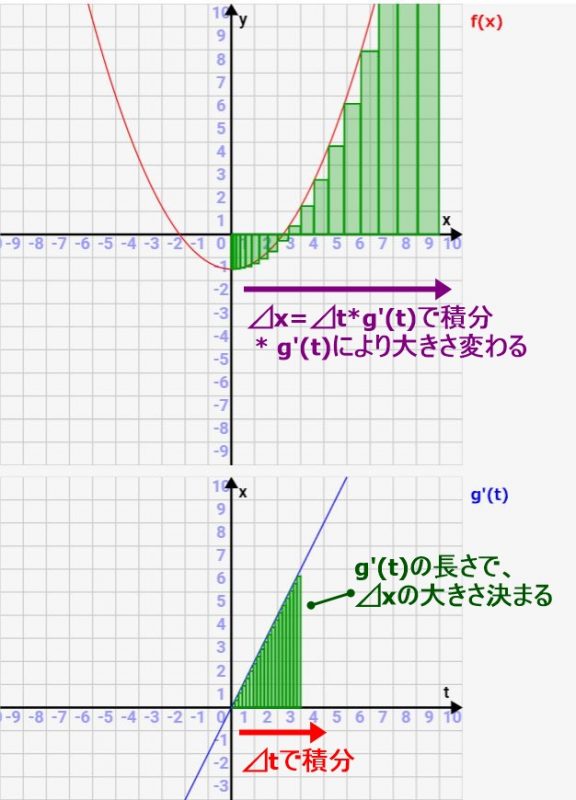
これは\(g(t)=t^2\)⇒\(g'(t)=2t\)で積分範囲をx=0~9とした場合の例です。上のグラフがf(x)で、↓のグラフがg'(t)です。
基本的には下のg'(t)の⊿tベースで積分されますが、⊿x=g'(t)*⊿tで⊿xに変換され、間接的に⊿xで積分することになります。
ここで重要なのが「g'(t)によって⊿xの大きさが変わる」ことです。通常のxでの積分では⊿xは一定ですが、合成関数の場合は⊿x=g'(t)*⊿tで間接的に計算されるため、↑のf(x)のグラフ中のように⊿xの大きさ(太さ)が異なるんです!その太さはg'(t)によって決まります。今回の例の場合、\(g'(t)=2t\)のため、tに比例して⊿xの太さが大きくなっています。
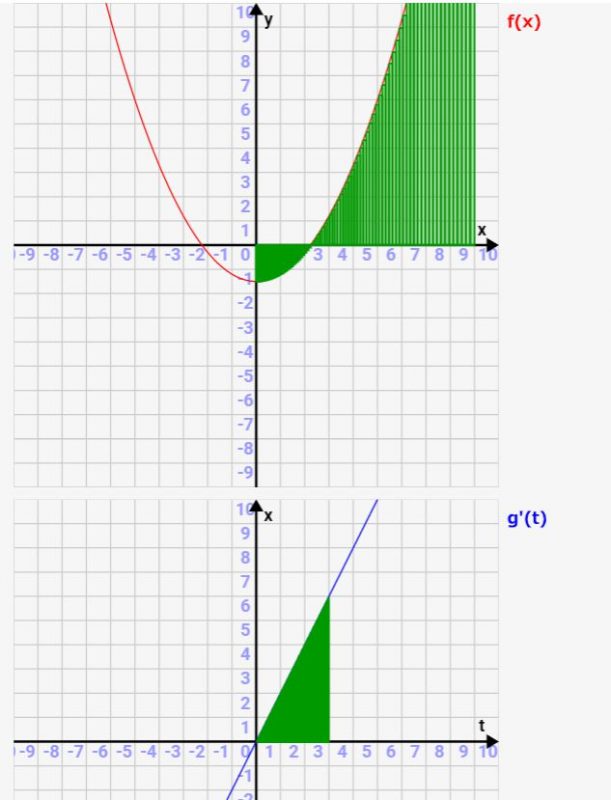
ただ、最終的に⊿tを小さくしていくと、、、↓のように通常の積分での面積計算と変わらなくなります。⊿xの大きさは異なりますが、普通の積分と同様にf(x)の面積が網羅できるんです。そのため、通常のxでの積分(\(\int f(x) dx\))と同値になるんです!
また、上の例を見るとわかるように、⊿tと⊿xは太さや位置が違うため、積分対象区間も変わります。変数tベースでの積分になるため、x=α~βに対応したt=α’~β’が新たな積分対象範囲になるんですね!
置換積分の注意点
置換積分により、どんな変換をしても基本的には良いのですが、いくつか注意点があります。
変数x=g(t)で、少なくとも定積分の定義域は網羅できないといけない
例えば、x=-2~4の定積分なのに、t=x^2という変換をしようとすると、、、x=-2に対応するtの解が存在しなくなります。こうすると定積分が不可能になります。少なくともx=α~βの範囲で、対応する解のあるg(t)を選ばないといけないです。
置換積分シミュレーター!合成関数の積分のイメージを「⊿x=g'(t)*⊿t」という観点で、理解しよう!
シミュレーターの説明
上記で説明した合成関数での積分のイメージを、シミュレーターで確認してみましょう!前回の通常積分の面積計算と同様、x=α~βの範囲を、n等分して面積計算するイメージです。ただ、上記のように⊿tをベースにして⊿xの太さが決まるようになっています。
積分対象となる元の関数f(x)は↓の二次関数で固定です。
\( {f(x)=} \) + 1\( {x^2 } \) + 1
それに対して、変換関数g(t)は↓のa,b,cのパラメタを指定して自由に変更できます。
また、積分対象を決めるのα(xの下限),β(xの上限)やn(分割数)もスライドバーで指定可能です。変換関数g(t)を変更して、どのように⊿xの太さが変わるのか確認しましょう!また、実際の積分値と、面積の値との誤差が、nが大きくなるほど小さくなることを確認しましょう!
置換積分シミュレーター
↓のスライドバーでg(x)の関数や、積分区間α~βを調整した後、分割数nの値を上げてみましょう!
\( {g(t)=} \) + 1\( {t^2 } \) + 1\( {t } \) + 1
\( {g'(t)=} \) + 1\( {t } \) + 1
↓nが大きくなるほど、積分値(上)と面積が近くなることを確認しましょう!
= 0.0
まとめ:置換積分(合成関数の積分)は⊿xの太さがかわる!
上記の通り、置換積分とは合成関数の積分のことを意味しているんです。難しく、イメージが湧きにくい分野ですが、、、、↑のように⊿x=g'(t)*⊿tと考えれば、分かりやすいです!
この置換積分は物理の世界でも頻出する要素なので、↑のシミュレーターで理解を深めてもらえればと思います!
⇒「積分」カテゴリ記事一覧
その他関連カテゴリ