積分の意義を、物理の「位置 – 速度」シミュレーターで理解しよう![数学・物理入門]
数学の前回の記事までで、積分の基本的な考え方について説明しました。ただ、いまいち何のために積分をするのかが分かりにくいかと思います!
このため、物理の記事で説明してきた「位置 – 速度」の関係を例にして積分の意義を説明していきます!
![積分の意義を、物理の「位置 – 速度」シミュレーターで理解しよう![数学・物理入門]](https://retu27.com/wp-content/uploads/rapture_20210424220307-500x472.jpg)
目次
「位置 – 速度」は微分・積分の関係にある!
物理の世界では「位置 – 速度」の関係で物体の位置の変化を表します。速度の一般的な定義は↓になります。
\( \displaystyle 速度[m/s] = \frac{距離[m]}{時間[s]} \)
つまり、10秒間で100m進む物体の速度は10m/sとなります。簡単ですね。ただ、これは大まかな速度の定義なのです。速度をもっと、細かい単位で区切って定義することを考えます。すると微小量時間⊿tと微小量距離⊿xを使って↓のように定義できます。
\( \displaystyle 速度[m/s] = \frac{距離⊿x}{時間⊿t} \)
今、位置がf(t)で得られるものとすると、上記式は↓のように変形できます。
この⊿tが極限まで0に近くなると、t時点の速度が定義できるはずです。そのため、↓が正しい「t時点での速度」の定義になります。
これって、↓の導関数(微分)の定義そのものです。「速度関数は距離関数の導関数」という関係にあるんです。
↓導関数の定義。上記の速度の定義と全く同じ
$$ \large{ f'(x) = \displaystyle \lim_{ h \to 0 } \frac{f(x+h) – f(x)}{h} }$$
速度関数を積分すれば、位置が求められる!
上記のように「速度関数=距離関数の導関数」です。ですので、速度をf(t) とすると、その原始関数F(t)が位置を表す関数になるんです。
↓の図は右側が速度関数f(t)、左側が位置関数F(t)です。このように、速度関数を積分すると、位置を表すF(t)が求められるんです!
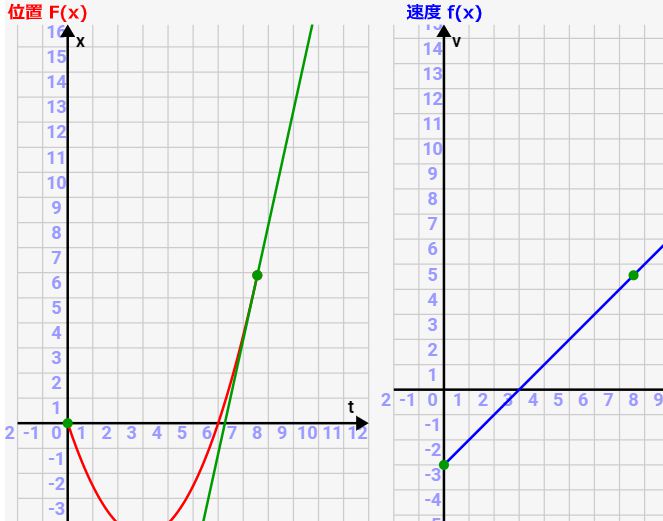
注意点としては、今までの積分で説明したとおり、「積分では定数Cの情報が抜け落ちているため、積分定数Cという不定項を使って表すしかない」という点です。
「位置 – 速度」の関係でいくと、「積分定数C=初期位置」という関係にあります。位置を微分すると、速度の関数が得られます。速度関数を見ると、物体がどう動くかわかります。しかし、「最初に物体がどこにあったか」は速度を見ても分からないですよね!それこそが不定項である積分定数Cなんです!
なので、積分を使う時は↓のどちらかのパターンになります。
2. 「t時間のうちに、どの程度動いたか」という変化に着目して計算する(定積分)
2.は初期位置がわからなくても、「ある時間帯でどの程度動いたか」は速度関数から求められるからです。この場合は初期位置\(x_0\)の情報は不要です。これこそが前回の記事で説明した定積分の考え方そのものです!
「位置 – 速度」シミュレーター!定積分のイメージを理解しよう!
上記で説明した「位置 – 速度」をシミュレーターを用いて確かめてみましょう!
- スライドバーで↓の速度関数f(t)のa,b,cのパラメタを自由に変更できます
- 指定されたf(t)をt=0~10の間で積分し、F(t)を計算して出力します
- 同時にアニメーションで物体の動きを表示します
- t=0~10の定積分の値も同時に出力されます
- チェックボックスで接線表示をON/OFFできます
「位置 – 速度」シミュレーター
積分で距離関数がどのように計算されるか、シミュレーターを用いて確認して見ましょう!また積分定数を変えても、定積分の値は全く変わらないことを確認しましょう!
\( {f(t)=} \) + 1\( {t^2 } \) + 1\( {t } \) + 1
\( {F(t)=} \) + 1\( {t^3 } \) + 1\( {t^2 } \) + 1\( {t } +C \)
= 0.0 – (0.0) = 0.0
↓値を変えると、自動的にアニメーションが始まります!
↑動的に再生速度を変えられます。左端で0にすると、一時停止となります。
まとめ:積分を使うと、速度関数から位置を簡単に求められる!
今まで積分について解説してきましたが、いまいちその有効性が分かりくかったと思います。
今回はその実例として「位置 – 速度」の関係を微分・積分の例として示しました。積分を使うと、速度関数f(t)と初期位置\(x_0\)さえわかれば、位置は求められるんです!
この微分・積分の関係を知っておくと、物理の様々な公式がより理解できるようになるのです。
- 微分積分の最たる例が位置/速度の関係
- ある区間で移動した距離は速度の積分から求められ、初期位置が分かれば到達位置まで特定できる
⇒「積分」カテゴリ記事一覧
⇒「速度・加速度」カテゴリ記事一覧
その他関連カテゴリ