難しい「余弦定理」をシミュレーターを使って理解しよう![数学入門]
目次
難しい余弦定理について解説します!
今回は余弦定理についてシミュレーターを使って解説します。余弦定理は三平方の定理を一般三角形に拡張したバージョンです。余弦定理になるとやや複雑です。
ただ、考え方は一緒。余弦定理をマスターすれば、色んな場面で三角形の辺の長さを求めたり、なす角θを求めたり出来るようになります!
![難しい「余弦定理」をシミュレーターを使って理解しよう![数学入門]](https://retu27.com/wp-content/uploads/rapture_20201215213743-500x429.jpg)
三平方の定理が使える条件
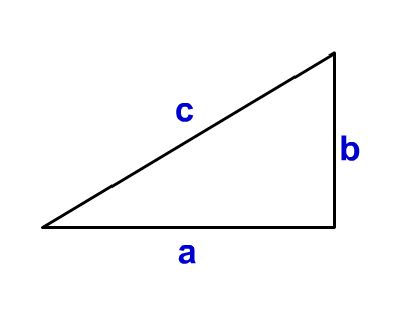
三平方の定理では、↓のような直角三角形において、二辺(例えば底辺と縦辺) から、もう一辺(斜辺)を求めることができました。(詳しくはコチラのページ参照)。さらにそこから各角度も計算することが出来ました。
直角三角形の斜辺cとその他二辺a,b(↓のような直角三角形)において、以下の式が必ず成り立つ
\( \displaystyle c^2 = a^2 + b^2 \)
しかし、この三平方の定理が使える↑のような「直角三角形」のときだけです。
直角三角形以外の場合はどうする?
それでは「直角三角形以外」の場合はどうやって求めればいいでしょうか?その悩みに答えるのが余弦定理です。
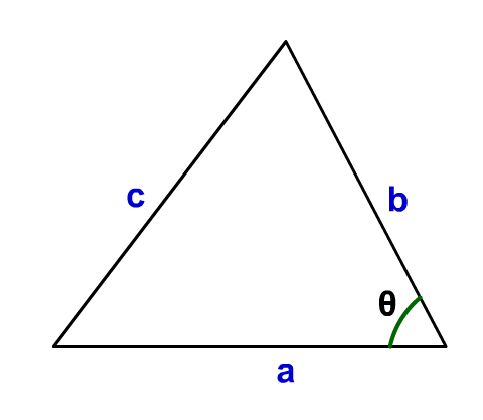
a,b,cが3辺の三角形において、aとbがなす角がθのような三角(↓図のような三角)がある時、↓の式が常に成り立つ
\( \displaystyle c^2 = a^2 + b^2 -2ab \cdot cosθ \)
三平方の定理は直角三角形の時にだけ使えましたが、この余弦定理は一般的な普通の三角形でも成り立つ公式です。この式を使えば、aとbとそのなす角θがわかれば、残りの辺cの長さも計算出来てしまうわけです!
やや複雑ですが、直角三角形以外にも適応できるので色んなときに活用できます!
余弦定理の証明
それでは、上記の余弦定理を証明していきます。基本的に考え方は「普通の三角形を、計算可能な直角三角形に分解する」です。
今回↓のような一般的な三角形を考えていきます。もちろん、角は直角ではありません。
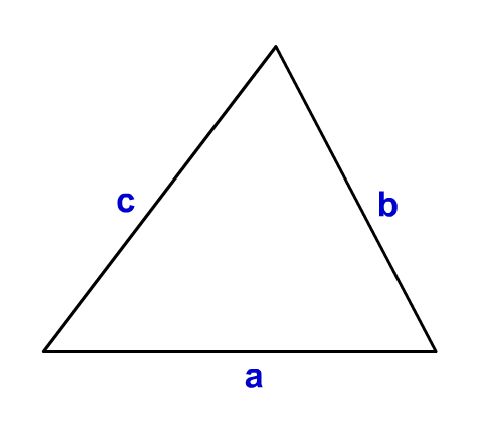
これを↓のように2つに分割して直角三角形を2つ作ります。こうする事で、三平方の定理やcos/sinの変換が、使えるようになり各辺が計算可能になるんです!

すると、コチラのページで解説している通り、直角三角形定義から↓のように各辺が求められます。これで右側の三角形は全ての辺の長さが求まりました。
あとは左側三角形の底辺だけ。ココは↓のように底辺同士の差分を計算すればよく、ピンクの右側三角形の底辺は、(a – b*cosθ)である事がわかります。
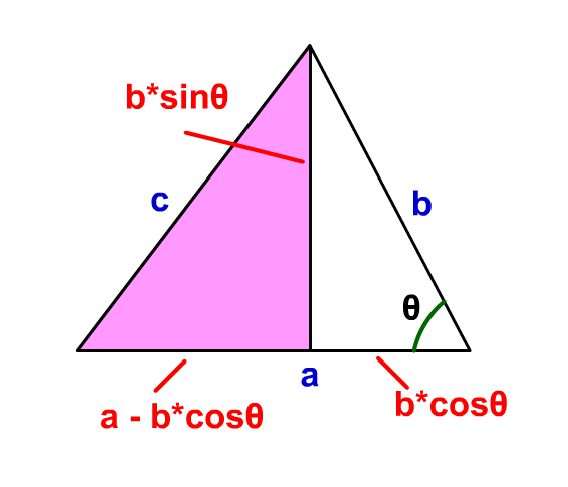
ここで↑の図のピンクの三角形に着目します。すると、三平方の定理から
が成り立つといえます。この式を解いていくと、、、
↓分解
\( c^2 = b^2 sinθ^2 + a^2 – 2ab cosθ + b^2 cosθ^2 \)
↓整理
\( c^2 = a^2 + b^2 (sinθ^2 + cosθ^2) – 2ab cosθ \)
↓ 定理\(sinθ^2 + cosθ^2 = 1\)を代入
\( c^2 = a^2 + b^2 – 2ab \cdot cosθ \)
となり、余弦定理が証明できたワケです!うまく直角三角形に分解して、三平方の定理を使って公式を導いているわけですね!
余弦定理は三平方の定理を包含している
今回示した余弦定理ですが、実は三平方の定理を包含しています。なぜなら、↓の余弦定理において、直角三角形ではθ=90°となるからです。
90°ならばcosθ=0なので、\(- 2ab \cdot cosθ\)の項が消えて、
になります。これはまさしく三平方の定理と同じですね!
ということで、「余弦定理は三平方の定理を一般化した式」と言えるわけです!三平方の定理は直角三角形限定でしか使えなかったのを、一般化したのがこの余弦定理なのです!
3辺の長さが分かっている時は、cosθ,θを求めることが出来る!
余弦定理は↓のような公式ですが、
三辺の長さがわかっている場合は、この式を変形して
\( \displaystyle cosθ = \frac{a^2 + b^2 – c^2}{2ab} \)
と、cosθが計算できてしまうのです!三角形の場合は\(0 ≦ cosθ ≦ 1\)なので、角度θは一意に求めることが可能です。
余弦定理をシミュレーターで理解しよう!
それでは上記で示した余弦定理を、シミュレーターで確認してみましょう!シミュレーターは1)2辺とそのなす角度θからもう一辺を求めるシミュレーターと、2)3辺から角度θを求めるシミュレーターを用意しています。どちらもよく使うパターンなので、必ず理解しましょう!
1)2辺とそのなす角度θからもう一辺を求めるシミュレーター
コチラのシミュレーターでは2辺とそのなす角度θを指定すると、もう一辺が計算され、三角形が描かれます。
↓の値を変えると、三角形の「辺a(底辺,緑)」「辺b(赤)」と「そのなす角度θ」を変更できます。これらの値を元に、↑で解説した余弦定理に当てはめて「もう一辺c(青色)」を計算します。
これらの値を変化させて、辺cの長さがどう変わるか確認してみましょう!!
2)3辺から角度θを求めるシミュレーター
次に3辺を指定すると、なす角度を計算してくれるシミュレーターです。
↓で辺a、辺b、辺cの値をかえると、自動的に余弦定理を使って角度θを計算し、三角形を描画してくれます。色々値を変えて、角度θがどうかわるか確認してみましょう!
(なお、コチラのページで解説している通り、三角形の成立条件があるので描画できないパターンもあります。ご注意を!)
角度θ:
まとめ:余弦定理は三平方の定理の拡張版。どんな三角形でも残りの一辺や角度が求められる!
最後にまとめです。前回説明した三平方の定理は便利ですが、「直角三角形でのみ使える」という強い制約がありました。
今回解説した余弦定義はこの「三平方の定理」の拡張版です。これを使うと、普通の直角でない三角形の場合も計算できます。
すごく便利ですので、難しいですが必ず理解するのをおすすめします!
- 三平方の定理を、直角三角形でない三角形にまで広げたのが「余弦定理」
- 二辺とその角度θがわかっていれば、残りの一辺が計算できてしまう
- 逆に三辺の長さがわかっていたら、余弦定理で角度θが計算できる
⇒「三角関数sin/cos/tan」カテゴリ記事一覧
⇒「幾何学・図形」カテゴリ記事一覧
その他関連カテゴリ