「ヘロンの公式(三辺から面積を求める)」をシミュレーターを使って理解しよう！[数学入門]

2021-02-06　

幾何学・図形

1 ヘロンの公式を解説します！
2 ヘロンの公式とは
3 ヘロンの公式の証明
4 ヘロンの公式シミュレーター
5 まとめ：各公式を適応していくと、ヘロンの公式というシンプルな形で面積計算できるようになる！

ヘロンの公式を解説します！

前回までに、三角形の面積の公式や、cos/sinの使い方、三平方の定理/余弦定理などを学んできました。実はこれらを組み合わせると、三角形の三辺の長さから、三角形の面積を直接計算することが出来るのです！

今回はその計算手順について解説します！最終的にはヘロンの公式という、簡単に面積を求められる公式を導いて行きます！
「ヘロンの公式(三辺から面積を求める)」をシミュレーターを使って理解しよう！[数学入門]

ヘロンの公式とは

まず、三角形の面積を順番に求めていく前に、最終的に導きたいヘロンの公式を紹介しておきます。

ヘロンの公式

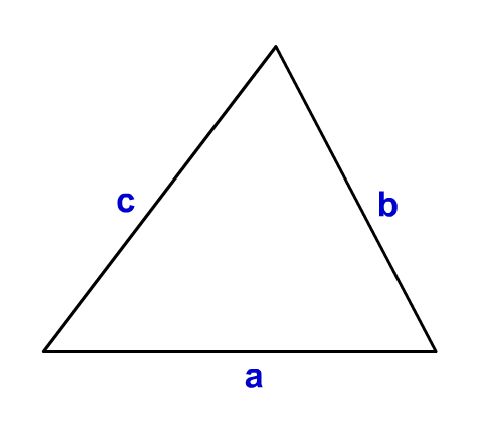
↓図のような三角形の三辺の長さをa,b,cとして
$\displaystyle s = \frac{a + b + c}{2} $
としたときに、三角形の面積は以下の公式で求められる
$\displaystyle 面積 = \sqrt{s(s-a)(s-b)(s-c)} $

途中で$ \Large{ s = \frac{a + b + c}{2} } $を計算していますが、これは計算を簡単にするためです。このsをつかうと、こんなに綺麗に三角形の面積は求めることが出来るのです！

ヘロンの公式の証明

それではヘロンの公式を証明していこうと思います。今まで求めてきた公式をたくさん組み合わせて求めていきます。

三角形の面積は「底辺×高さ÷2」で求められる

これはコチラのページでも解説していますが、三角形の面積計算の基本ですね。

三角形の面積の公式

$ \displaystyle 三角形の面積 = 底辺の長さ × 高さ ÷ 2 $

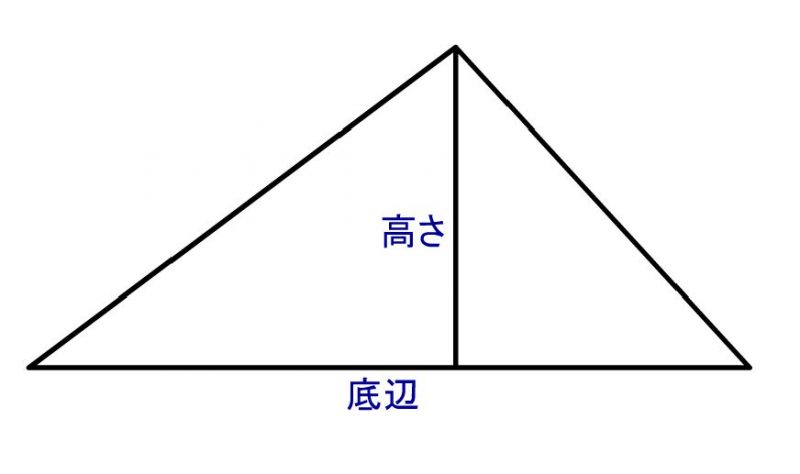
どんな形の三角形も、底辺と高ささえ分かれば面積計算できるんです。

三角形の高さは「斜辺×sinθ」で求められる(cos/sinの活用)

それでは三角形の高さはどのように求めればいいでしょうか。それは、例えば三角形の辺を↓のようにa,b,cで名付けた時、aとbのなす角θが分かれば求められます。

コチラのページで詳しく解説していますが、斜辺bにsinθを掛けると高さを求めることが出来ます。

三角形の面積の公式

$ \displaystyle 高さ = b × sinθ $

これは↑のように三角形を2つ二分割したとき、それぞれ直角三角形とみなすことが出来るからです。直角三角形であれば、θを使えば斜辺から底辺や高さがcos/sinを使って求められるんですね。

ただ、このsinθをどうやって求めるかですよね＞＜

cosθは三辺の長さから求められる(余弦定理)

上記の通り、sinθがわかれば面積は求められます。そして、三辺a,b,cの長さが分かっているならば、cosθならすぐに求められます。前回説明した、余弦定理を使うのです。

余弦定理でcosθを求める式

$ \displaystyle cosθ = \frac{a^2 + b^2 – c^2}{2ab} $

これを使えばcosθをすぐに求められます。ただ、sinθに変換しないといけないのですが、、、

sinθは定理を使えば簡単にcosθに変換できる

sinθとcosθはすぐに互いに変換が可能です。なぜなら、↓のような式がなりたっているからです。

三角関数cos/sinの公式

$$ \large{ cos(θ)^2 + sin(θ)^2 = 1 }$$

ですので、sinθは

$$ \large{ sinθ = \sqrt{1 – cosθ^2} }$$

で求められます（三角形のため、0≦θ≦180°という制約があるため、sinは+と断定できる）

上記の前提を使って、面積が三辺から計算可能！

これで準備は整いました。三角形の面積を三辺a,b,cから求めていきます。

$\displaystyle 面積 = 底辺(a)×高さ/2$

↓　$ \displaystyle 高さ = b × sinθ $を代入する

$\displaystyle 面積 = a * b * sinθ /2$

↓ $sinθ = \sqrt{1 – cosθ^2}$を代入

$\displaystyle 面積 = a * b * \sqrt{1 – cosθ^2} /2$

↓余弦定理$ cosθ = \frac{a^2 + b^2 – c^2}{2ab} $を代入

$\displaystyle 面積 = \frac{a * b }{2}* \sqrt{1 – (\frac{a^2 + b^2 – c^2}{2ab})^2} $

↓数式整理

$\displaystyle 面積 = \frac{1}{4}* \sqrt{(2ab)^2 – (a^2 +b^2 -c^2)} $

↓$(α^2 – β^2) = (α – β)(α + β)の公式適応$

$\displaystyle 面積 = \frac{1}{4}* \sqrt{(2ab + a^2 +b^2 -c^2)(2ab – a^2 -b^2 +c^2)} $

↓(a+b)^2と(a-b)^2の形で整理

$\displaystyle 面積 = \frac{1}{4}* \sqrt{((a+b)^2 -c^2)(c^2-(a-b)^2)} $

↓$(α^2 – β^2) = (α – β)(α + β)の公式再適応$

$\displaystyle 面積 = \frac{1}{4}* \sqrt{(a+b+c)(a+b-c)(c+a-b)(c -a +b)} $

　
　
キレイな形になってきましたね。そしてここで
$\Large s = \frac{a+b+c}{2}$
という変数を使ってまとめる事を考えます。すると

$\displaystyle 面積 = \frac{1}{4} * \sqrt{(2s) * (2s -2c)*(2s -2b)*(2s-2a)} $

↓$\frac{1}{4}$とルート内の係数2を相殺

$\displaystyle 面積 = \sqrt{s(s-a)(s-b)(s-c)} $

　
ということでヘロンの公式が出来上がりました！過程は長かったですが、最終的にはシンプルな形で公式が落ち着きます！
　

POINT各定理を組み合わせると、ヘロンの公式という便利なものが作れる！

ヘロンの公式シミュレーター

それでは実際にヘロンの公式を使って三角形の面積を求めてみましょう！

↓で辺a、辺b、辺cの値をかえると、自動的にヘロンの公式を使って面積を求めてくれます。

（なお、コチラのページで解説している通り、三角形の成立条件があるので描画できないパターンもあります。ご注意を！）

a(緑)

6.0

b(赤)

8.0

c(青)

4.0

s =
面積 =

まとめ：各公式を適応していくと、ヘロンの公式というシンプルな形で面積計算できるようになる！

最後にまとめです。三角形の面積は底辺×高さ÷2です。しかし、各辺の長さがわかっているけど、高さが分からないため面積が計算できない事があります。

そんな時には今回説明したヘロンの公式↓が役立ちます。

ヘロンの公式

$\displaystyle s = \frac{a + b + c}{2} $
としたとき
$\displaystyle 面積 = \sqrt{s(s-a)(s-b)(s-c)} $

この公式があれば瞬時に面積を求められます！上記の証明の通り、sinθを介して高さを求めていく過程が重要なので理解しておきましょう！
　

まとめ

ヘロンの公式を使うと、三辺の長さだけで三角形の面積が求められる

[関連記事] 数学入門：三角形に関する公式

1．三角形の成立条件

2．「三角形の面積(底辺×高さ÷2)」の復習

3．三平方の定理

4．余弦定理

5．ヘロンの公式(本記事)

⇒「幾何学・図形」カテゴリ記事一覧

その他関連カテゴリ

学問系TOP AI/ChatGPT 数学物理統計学コンピューター経済学 Webツール