平均とは何か?をシミュレーターを用いて詳しく解説!実験で深く理解しよう![統計学/確率入門]
本サイトでは、数学分野の内容を基礎から分かりやすくシミュレーターを用いて解説しています!このベースを用いて、以後「統計学/確率」の分野の内容を同様にシミュレーターを作って解説していきたいと思います!
統計学は最強の学問と呼ばれるぐらいどこでも応用が効く学問です。また、この統計学の内容は今流行りのAIの機械学習の考えにもつながってきます!しかし、、、複雑すぎてイメージしにくい事が多いんですよね><
ということで、本サイトではこの「統計学/確率」の内容を可能な限り分かりやすく、手で動かせるシミュレーターを用いて解説していこうと思います!
まず最初に基礎の基礎である「平均値」について、本記事では解説していきます!
![平均とは何か?をシミュレーターを用いて詳しく解説!実験で深く理解しよう![統計学/確率入門]](https://retu27.com/wp-content/uploads/rapture_20210228172221-500x371.jpg)
目次
「平均値」とは何か?改めて考えてみる!
本記事では「平均値」について考えていきます。日常会話でも「平均」って言葉を使いますよね。なんとなく「平均=真ん中の値」ってイメージあると思いますが、この定義を厳密に理解していきましょう!
前提:例として0~100点のテストの点の統計を考えて行きます!
本記事では、0~100点のテストの点の統計を例にして考えていきます!複数人がテストを受けた時の「テストの平均値」をどのように計算をしていけばよいか、考察していきます。
平均値の定義
まず、平均値の定義について解説します。その前にまず以下のように用語の定義をします。
\(x_i\): i番目の人の点数
これだけだと分かりにくいですが… 例えば、5人でテストを受けて出席番号1番の人が50点、2番の人が20点、3番の人が60点、4番の人が40点、5番の人が90点だとしたら
\( x_1 = 50 , x_2 = 20, x_3 = 60, x_4 = 40, x_5 = 90 \)
というように人数と点数を表現していきます。
この時に、平均値の定義は以下の式で表せます。
\( 平均値 \)
\( \displaystyle = \frac{1}{n}(x_1 + x_2 + … + x_n) \)
\( \displaystyle = \frac{1}{n}\sum_{i=1}^{n}x_i \)
一番最後のシグマΣの表記が分からない方は無視しても構いません(詳しくはコチラの記事で解説中!)。重要なのはこの式の意味です。つまりは、「全ての点数\(x_i\)を足して、データ個数nで割る」というのが平均の定義です。
上記の5人の場合の具体例で計算すると
\( 平均値 \)
\( \displaystyle = \frac{1}{5}(x_1 + x_2 + x_3 + x_4 + x_5) \)
\( \displaystyle = \frac{1}{5}(50 + 20 + 60 + 40 + 90) \)
\( \displaystyle = \frac{260}{5} \)
\( \displaystyle = 52 \)
となります。なんとなく真ん中っぽい値になりましたね(^^)
平均値の変動をシミュレーターで体感しよう!
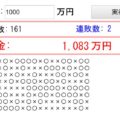
ここまで解説してきた「平均値」がどのように変動するのか、具体的な平均値のイメージをつけるためにシミュレーターを動かして実験してみましょう!
- スライドバーでn(人数、データ個数)を変えるとシミュレーターが動き出します
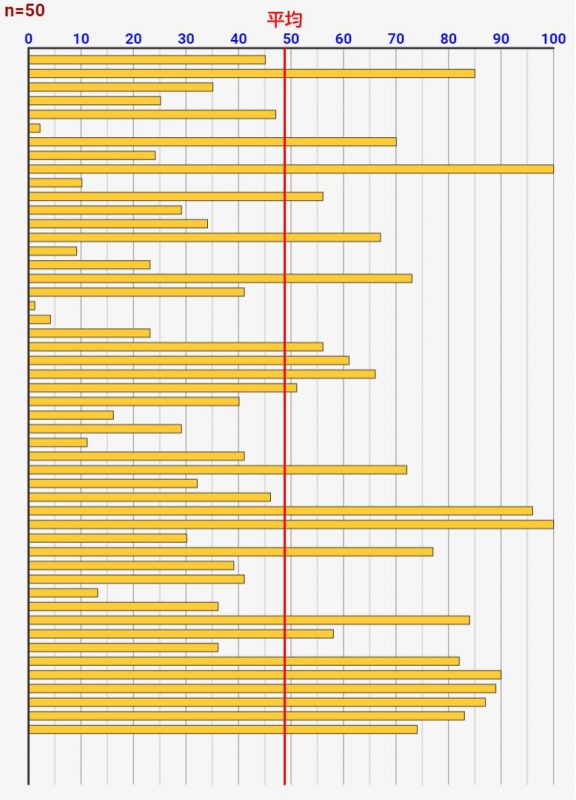
- シミュレーターはn人の点数を0~100までランダムで算出して、棒グラフとして点数を描画していきます
- 同時にリアルタイムに平均値が動いていきます
nを色々変えてみて、どのように平均値が動いていくかを確かめましょう!
平均値の重要な性質
上記のシミュレーターを動かしていくと分かりますが、以下のような性質があります!
性質1: nが小さい時は大きく変動して、nが大きくなると殆ど動かなくなる
n=2,3など小さい時は、点数0や100点の人が入ってくると大きく平均が変動します。しかし、n=50等、大きな数になってくると、点数0や100点といった極端な値が入ってきてもあまり変化しなくなります。
平均値はデータ個数nで割るので、データ数が多くなるほど1つのデータの影響度が小さくなってくるわけです!
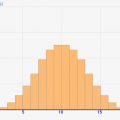
性質2: nが大きくなるほど、平均は50に近づいてくる傾向にある
これも重要な性質です。一概にそうなるとは限らないのですが、nが大きくなるとだんだんと50に平均値が近づく傾向にあります。
今回、0~100点の間でランダムで点数がつけられるので、数が大きくなっていくほど真の平均値である50に近づいて行くわけです。逆に言うと、n=2,3とデータ個数が少ない場合は平均=20といった値にもなるわけで。この性質は統計を考える上で重要になってきます!
性質3: 平均値は点数を均平化した値。n個足しても総和は変わらない
これも重要です。平均値をn個足すと
\( \displaystyle = \frac{1}{n}(x_1 + x_2 + … + x_n) \cdot n \)
\( \displaystyle = (x_1 + x_2 + … + x_n) \)
となり、結局、元の点数を全て足した数と変わらない事になります。つまり、上記のシミュレーターで表示されているオレンジの棒グラフの面積の総和は、平均値に平均化しても変わらないわけです。
このイメージをシミュレーターを用いて確認しておきましょう!
平均値で面積が均平化出来ることを理解しておこう!
- 上記のシミュレーターと同じように動きますが、最後に各グラフが平均値に均平化していきます
- 平均値より上の点数を減らし、平均値より下の配分に分け与えていくと、最終的に平均値で均平化されます
シミュレーターを↓データ個数nを変えて動かしてみて、この均平化前後で、面積が変わらないことを理解しておきましょう!
今度は自分でシミュレーターに点数を入力していき、平均値の動きを理解しよう!
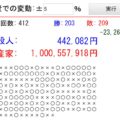
最後に、平均値の定義をシミュレーターで確認してみましょう。自分で点数を入力して実験ができます。入力したテスト点数により、どのように平均値が動くのか確かめましょう!
- スライドバーを動かし、指/マウスを離した時点でその点数が追加されます
- 入力した点数に従って、平均値がリアルタイムに変動します
- リセットボタンで初期化できます
ポンポン押しながらデータを追加していき、平均値の変動を確かめて見ましょう!
次回は「中央値」について解説します!
平均値は統計上「真ん中」を示す概念です。しかし、実は統計上は「真ん中」を示す値は平均値だけではないんです。
次の記事では、その一つである「中央値」について解説していきます!「真ん中」といっても、平均値だけではないのです!><
- 「平均値」は真ん中を表す重要な値
- 平均化しても、データの面積(総和)は変わらない
⇒「平均/分散等の代表値」カテゴリ記事一覧
その他関連カテゴリ