順列(P記号)をシミュレーターで理解しよう![数学入門]
この記事では、前回記事に続いて数学の基礎の「順列(並び順)」について解説していきます。今回は「n個のクジから、r個引くパターン」について、シミュレーターを用いて考察していきます。
そして、そのパターン数を表すP記号について、詳しく解説していきます!
目次
「n個のクジから、r個引くパターン」をクジ引きの例で理解しよう!
前回の記事では、n個のクジ全てを使って順列を作るパターンを考えていました。今回はそこから少し一般化して「n個のクジから、r個引くパターン」を考えてみます。n個全てを引くわけでなく、r個だけ引く場合を考えます。まず、この問題を表現したクジのシミュレーターでイメージつけましょう!
- 総数(n)と引く個数(r)を変えると、クジがランダムで引かれ、数列が作られます
数列が作られるパターンを観察しましょう!
前回の例とは違って、全部引かれるわけではないです(総数n=個数rにしたら、前回と同じです)
このような「n個のクジから、r個引くパターン」で、パターン総数を以下求めていきます!
順列(並び順)全パターン出力シミュレーターで、理解しよう!
上記で説明したn個のクジから、r個のクジを引くパターンで、どれだけのパターン数があるかシミュレーターでまずは見てみましょう!
- ↓の総数(n)と引く個数(r)を変更すると、その個数での順列パターンを全て列挙していきます
- 青色数字は前数列から変化があった範囲、灰色数字は前数列と変わらない範囲を示しています
- 個数が6以上になると、列挙に時間かかるので注意して下さい
色々数字を変えて、実験してみましょう!
*
…
上記のシミュレーターのように、順列のパターン数は総数(n)と引く個数(r)によって決まります。
結論から言うと、そのパターンの数は
\( {}_n P_r = n \cdot (n-1) \cdot … \cdot (n – r + 1) \)
通りになります。これを数学では\({}_n P_r \)という記号で表します。
具体例でいうと、総数n=9,個数r=3の場合は
通りになります。
パターン数が\({}_n P_r\)となるのは、パターンを考えれば分かります!
上記の通り、総数n個からr個引く順列の総パターン数は\({}_n P_r\)となります。これは上のシミュレーターでパターンを見れば分かると思います。
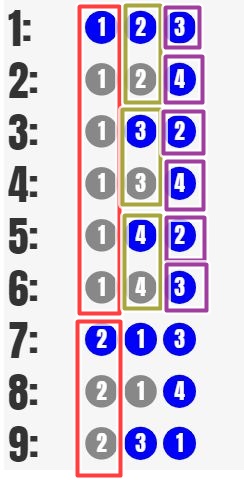
簡単に今、総数n=4から個数r=3個引く場合を考えます。この時、列挙されるパターンは以下の図のように区分できます。
まず赤線で囲った第一列目は、1,2,3,4の4パターンの値がきます(省略していて全部図示できてませんが)。各パターン場合分けをして考えます。次に第二列目を考えると、図の緑線の区分のように1列目の数字以外の3パターン(1列目が1の場合、それ以外の2,3,4)になるはず。さらに、3列目のパターンをみていくと、それぞれで1列目と2列目以外の数字の2パターンとなります。
つまり、全部で
パターンあるのが分かります。
総数nから個数rを引いていくと、1列目からn,n-1,n-2…と1つずつパターン数が減っていくわけですね!なので、繰り返しになりますが、全てのパターン数は
\( {}_n P_r = n \cdot (n-1) \cdot … \cdot (n – r + 1) \)
と表せるわけです!
- 「n個のクジから、r個引くパターン」は\( {}_n P_r = n \cdot (n-1) \cdot … \cdot (n – r + 1) \)パターンになる
- 最後までクジをひかないので階乗よりも少ないパターン数となる
⇒「順列/組み合わせ」カテゴリ記事一覧
その他関連カテゴリ