「ラザフォードの原子模型」エネルギーの変化をシミュレーターで理解しよう![物理入門]
コチラの化学の記事で、原子とはどういう構造なのかを説明しています。ただし、実際の原子はもう少し複雑な条件を満たしながら動いています。
今回は「ラザフォードの原子模型」でのエネルギーの変化について、シミュレーターを用いて解説していきます!
![「ラザフォードの原子模型」エネルギーの変化をシミュレーターで理解しよう![物理入門]](https://retu27.com/wp-content/uploads/20220612171338-404x500.png)
目次
おさらい:「ラザフォードの原子模型」とは
ラザフォードの原子模型とは「電子は原子核の周りを自由な軌道で回れるのではなく、一定の条件を満たさないと安定的に存在できない」という仮説を置いたものです。
実際に原子は連続的なエネルギーを持たず、とびとびのエネルギーしか持てないのです。そのため、↑のように何らかの存在条件があるのではと考えたわけです。
その条件とは↓のものです。これを「量子条件」といいます。
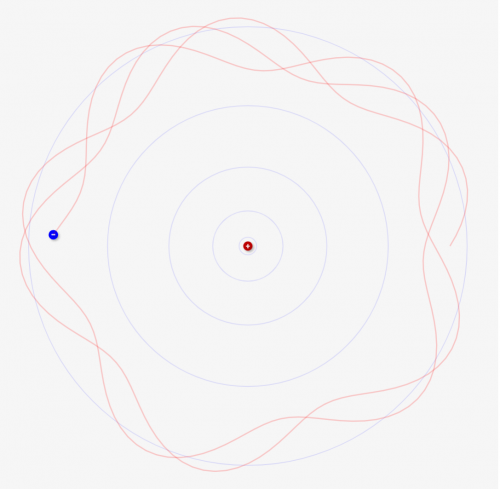
電子は波のように揺れており、電子が円上に周回しても同じ軌道をとる場合に安定して存在可能になる
↓
波の波長λ×定数倍n = 2πr
- \(r\) : 電子の軌道半径
これは↓のような状況になります。赤線が電子の軌道になります。電子は円上を周回しながら、↓のように左右に波のように揺れながら動いているんです。このときに、2周目、3周目に入っても同じ軌道をとって周回するときにだけ、安定的に電子が存在できるというのが量子条件です。
そして、これを満たすのは「円周の長さ 2πr」が「左右に揺れる波の波長」の定数倍になるときなんですね!

この条件を満たさない場合は↓のように、2周目3周目と違う軌道をとってしまいます。この場合電子は不安定になり、別の軌道に移動しようとするんですね。だからこそ、安定的な軌道はとびとびの位置にしかないんです。
「ラザフォードの原子模型」のエネルギーを求めてみる
前回記事では、電子軌道の半径rについて求めましたが、今回はエネルギーについて考えてみます。
まず前回求めたように、半径rは↓のような式で表せます。
\( \displaystyle r = \frac{h^2}{4π^2mke^2}n^2 \)
- \(h\) : プランク定数
- \(m\) : 電子の質量
- \(k\) : クーロン力係数
- \(e\) : 電子の電荷
- \(k\) : クーロン力係数
ここで電子の力の釣り合いについて変形すると、運動エネルギー\(\frac{1}{2}mv^2\)が↓のように求められることがわかります。
\( \displaystyle ma = \frac{ke^2}{r^2} \)
↓円運動時にかかる加速度は\(\frac{v^2}{r}\)
\( \displaystyle \frac{mv^2}{r} = \frac{ke^2}{r^2}\)
↓変形
\( \displaystyle \frac{1}{2}mv^2 = \frac{1}{2}\frac{ke^2}{r}\)
- \(v\) : 電子の速度
- \(m\) : 電子の質量
- \(r\) : 電子の軌道半径
- \(k\) : クーロン力係数
- \(e\) : 電子の電荷
また、電荷による位置エネルギーは、こちらの電荷エネルギーの記事で解説しているように、↓のように求められます。電荷としてみると、陽子の電荷がe、電子の電荷が-eとなるためです。
マイナスで表現されている通り、r=∞となる無限遠が基準値となりエネルギー=0になることに注意して下さい!
\( \displaystyle エネルギーU = – \frac{ke^2}{r} \)
- \(k\) : クーロン力係数
- \(e\) : 電子の電荷
ここで電子のエネルギー全体を考えてみると、そのエネルギーは「運動エネルギー + 電荷の位置エネルギー」で表せるので、↓のように変形できます。
エネルギー = 運動エネルギー + 電荷の位置エネルギー
↓代入
= \( \displaystyle \frac{1}{2}\frac{ke^2}{r} – \frac{ke^2}{r}\)
= \( \displaystyle -\frac{1}{2}\frac{ke^2}{r}\)
- \(k\) : クーロン力係数
- \(e\) : 電子の電荷
このようにシンプルな形で電子のエネルギーは表せるのです!さらにこれに↑で求めていた「円運動の半径r」を代入すると↓のように求められます。
\( \displaystyle U = – \frac{2π^2k^2me^4}{n^2h^2} \)
- \(h\) : プランク定数
- \(m\) : 電子の質量
- \(r\) : 電子の軌道半径
- \(k\) : クーロン力係数
- \(e\) : 電子の電荷
重要なのはエネルギーが量子数nの二乗に比例してマイナス値が小さくなる、つまり大きくなるということです。エネルギーとして最低なのがn=1のときであり、量子数nが増えるほどエネルギーは増えていくんです!
「ラザフォードの原子模型」のエネルギーをシミュレーターで確認してみよう!
それでは「ラザフォードの原子模型」でn=1,2,3…のときにエネルギーがどのように変化するか実際に確かめてみましょう!
エネルギーは基準点を0として表現しています。
- ↓のスライドバーで量子数nを変更すると、波長λ = 2πr/n の軌道に電子が移動しはじめます(nは整数のみ指定可能)
- グラフ上では、現在のエネルギーがどの位置かを示しています(赤線が基準点=0)
- 量子数nの増減で、エネルギーが上下する様子を確認してみましょう!
まとめ:エネルギーはn=1から上昇していき、基準点=0エネルギーに収束していく!
↑のシミュレーターを動かすと、量子n=1では大きなマイナスであったエネルギーが少し増やすだけで急激に増えることが分かると思います。エネルギーのマイナス分がnの二乗に反比例するので、n=2,3となると↓のように急激にエネルギーが上昇するわけです。

ただし、そのエネルギー上昇値は量子数nが増えていくと急激に減っていきます。↑のようにnが大きくなっても、最終的に基準点=0に近づくだけであるため、上昇値は限られるわけです。
つまり、n=1,2,3とか小さな値の間では急激にエネルギーが変わるんです!
⇒「原子」カテゴリ記事一覧
その他関連カテゴリ










