「ラザフォードの原子模型」をシミュレーターで理解しよう![物理入門]
コチラの化学の記事で、原子とはどういう構造なのかを説明しています。ただし、実際の原子はもう少し複雑な条件を満たしながら動いています。
今回はそのモデルである「ラザフォードの原子模型」について、シミュレーターを用いて解説していきます!
![「ラザフォードの原子模型」をシミュレーターで理解しよう![物理入門]](https://retu27.com/wp-content/uploads/20220612094049-500x489.png)
目次
原子とは?
原子とは、「この世界を構成する最小要素」です。地球にあるもの、宇宙にあるものの全てがこの「原子」で構成されます。
世界にある水や金属、生物など全く違うものに見えますが、細かく見ていくと全て原子で構成されているんです!
原子は↓のような構造になります。
赤で示している陽子、緑で示している中性子、青で示している電子の3つの要素で構成されるんです。電子は原子核の周りを円運動して周回しているイメージになります。
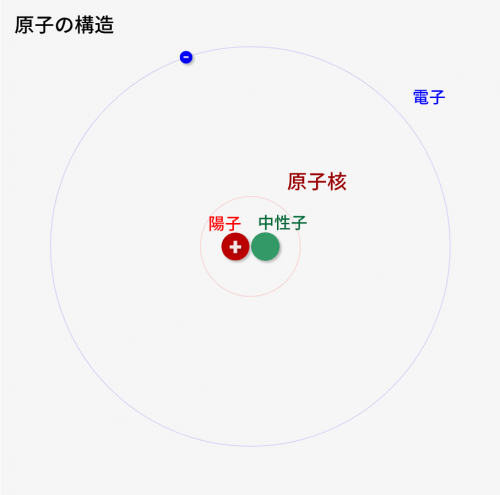
このうち、陽子、中性子は中心に配置されており、2つ合わせて原子核と呼びます。
各要素は↓のような性質があります。
陽子
- 中性子とともに、中心(原子核)を構成する要素
- 中世子と同じ質量を持つ
- 電子とは真逆のプラスの電荷をもつ
中性子
- 陽子とともに、中心(原子核)を構成する要素
- 陽子と同じ質量を持つ
- 電荷をもたない
電子
- 原子核のまわりを回る要素
- 陽子とは真逆のマイナスの電荷を持つ
- 陽子/中性子と比べると小さく、質量がほとんどない
「ラザフォードの原子模型」とは
ラザフォードの原子模型とは「電子は原子核の周りを自由な軌道で回れるのではなく、一定の条件を満たさないと安定的に存在できない」という仮説を置いたものです。
実際に原子は連続的なエネルギーを持たず、とびとびのエネルギーしか持てないのです。そのため、↑のように何らかの存在条件があるのではと考えたわけです。
その条件とは↓のものです。これを「量子条件」といいます。
電子は波のように揺れており、電子が円上に周回しても同じ軌道をとる場合に安定して存在可能になる
↓
波の波長λ×定数倍n = 2πr
- \(r\) : 電子の軌道半径
これは↓のような状況になります。赤線が電子の軌道になります。電子は円上を周回しながら、↓のように左右に波のように揺れながら動いているんです。このときに、2周目、3周目に入っても同じ軌道をとって周回するときにだけ、安定的に電子が存在できるというのが量子条件です。
そして、これを満たすのは「円周の長さ 2πr」が「左右に揺れる波の波長」の定数倍になるときなんですね!

この条件を満たさない場合は↓のように、2周目3周目と違う軌道をとってしまいます。この場合電子は不安定になり、別の軌道に移動しようとするんですね。だからこそ、安定的な軌道はとびとびの位置にしかないんです。
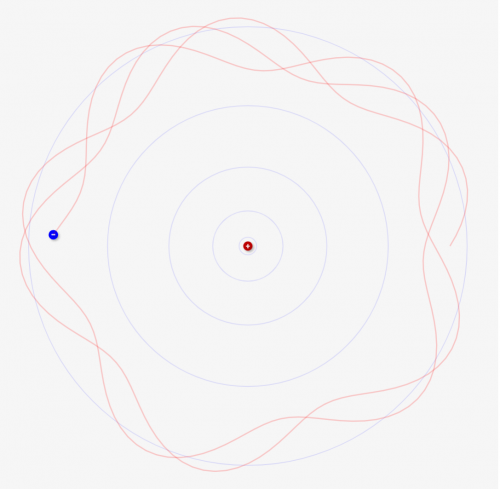
具体的には半径rは↓の条件を満たす位置にだけ存在することになります。n=1,2,3…と整数になるため、rは非連続的な値をとるわけです。
\( \displaystyle r = \frac{λn}{2π}\) (n=1,2,3…)
ここでこの整数となるn=1,2,3…を量子数といいます。量子数nが変わると軌道が変わるわけですね。
次回の記事で詳しく説明しますが、実際には波長λは周期によって変わり、半径rは量子数nの二乗に比例することになります。↓の青線が実際に電子がとれる半径/円周軌道になるわけです。

「ラザフォードの原子模型」をシミュレーターで確認してみよう!
それでは「ラザフォードの原子模型」がnが定数倍のときに安定することを、シミュレーターで確認してみましょう!
- ↓のスライドバーでnを変更すると、波長λ = 2πr/n の条件で電子が動き始めます
- 量子数nが整数になるときだけ、周回しても同じ軌道になり、安定的に電子が周回することを確認してみましょう!
まとめ:電子は「量子条件」を満たさないと存在できない!
↑のシミュレーターを動かすと、n=1,2,3,4,5と整数のときだけに安定的に同じ軌道を通ることがわかると思います。
少しでもそこからズレると、↓のように違う軌道を電子が通ってしまい、不安定になって存在できなくなるわけです!
↓n=4.9の例。周回する度に少しずつ軌道がズレるため、不安定となる

⇒「原子」カテゴリ記事一覧
その他関連カテゴリ










