「二次方程式(二次関数)の解の公式」をシミュレーション/図解で理解![数学入門]
前回記事で、\(ax^2 + bx + c = 0\)の解の個数を判別する式の説明をしました。今回は実際に解を算出する「二次方程式の解の公式」について説明します!
![「二次方程式(二次関数)の解の公式」をシミュレーション/図解で理解![数学入門]](https://retu27.com/wp-content/uploads/20220226105628-500x500.png)
目次
おさらい:二次関数の「平方完成」と「解の判別式」
二次関数は↓の形式で表せる関数です。a=0だと一次関数になるため、以後a≠0の前提で説明します。
$$ \large{y = ax^2 + bx + c }$$
この式は↓のように変形できます。
$$ \large{y = a(x + \frac{b}{2a})^2 -\frac{b^2 -4ac}{4a} }$$
これを平方完成形といいます!この形は、\(y=ax^2\)を\(y=a(x -B)^2 + C \)の形で平行移動したものと言えます。
故に、二次関数の頂点が↓だと分かるんです!
\( \displaystyle \large{ (B,C) = (-\frac{b}{2a}} , -\frac{b^2 -4ac}{4a}) \)
この頂点の位置を考慮すると↓の判別式が導けます(詳細は前回記事)
\(\Large{D=b^2 -4ac}\) としたとき、
D < 0 ⇒ 解無し(二次関数はx軸と交わらない)
D = 0 ⇒ 解1つ(二次関数とx軸が接する)
D > 0 ⇒ 解2つ(二次関数とx軸が交わる)
「二次方程式の解」とは?
二次関数の解を求めるとは、↓のように「y=0になる場合のxを求める」ことです。
$$ \large{y = ax^2 + bx + c = 0}$$となるxを求めること
つまり、↓のようにx軸と二次関数の交点(青い点)を求めることを意味します!
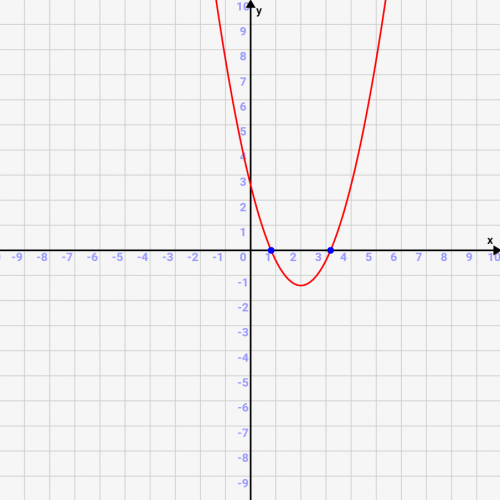
実際に二次方程式の解を求めてみる
この解を求めるために、平方完成の形を使用します。
$$ \large{y = a(x + \frac{b}{2a})^2 -\frac{b^2 -4ac}{4a} }$$
これがy=0になるxを求めていくと、、、
↓定数項移動
\(\displaystyle \large{a(x + \frac{b}{2a})^2 = \frac{b^2 -4ac}{4a}}\)
↓aで割る
\(\displaystyle \large{(x + \frac{b}{2a})^2 = \frac{b^2 -4ac}{4a^2}}\)
↓二乗部分の解をルートをつかって表す
\(\displaystyle \large{ x + \frac{b}{2a} = \pm \frac{\sqrt{b^2 -4ac}}{2a}}\)
↓左辺の定数を右辺へ
\(\displaystyle \large{ x = \frac{ -b \pm \sqrt{b^2 -4ac}}{2a}}\)
となります!これが二次方程式の解の公式です!プラスマイナスが入っているので、解が2つあるということを示しています!
$$ \large{ x = \frac{ -b \pm \sqrt{b^2 -4ac}}{2a}} $$
「二次方程式(二次関数)の解の公式」と「解の判別式」の関係
↑のような公式になりますが、前回記事で説明した通り、この方程式に必ず解があるとは限りません。
解があるかどうかは↓で判別できます。
\(\Large{D=b^2 -4ac}\) としたとき、
D < 0 ⇒ 解無し(二次関数はx軸と交わらない)
D = 0 ⇒ 解1つ(二次関数とx軸が接する)
D > 0 ⇒ 解2つ(二次関数とx軸が交わる)
これをみると、判別式Dが↓解の公式のルートの中の式と一致していることが分かります。つまり、解の判別式とは「解の公式のルート部分が正となり、解が存在するかどうか判定する式」でもあるんです!
$$ \large{ x = \frac{ -b \pm \sqrt{b^2 -4ac}}{2a}} $$
Dがプラスなら解は2つとれます。しかしDがマイナスならそんな解ないはずですし、D=0ならルート部分は消えるので、解は1つしかないことになるんです!
「二次方程式(二次関数)の解の公式」をシミュレーターで理解しよう!
それでは解説してきた、「二次方程式の解」の考え方をシミュレーターで確認してみましょう!
\(\large{y = ax^2 + bx + c}\)という二次関数をシミュレートできます!
- ↓でa,b,cを指定すると、二次関数がグラフ表示されます
- x軸との交点(y=0解の位置)を青点で示しています
- 解xが↑で説明した解の公式に当てはまっていることを確認しましょう
- 判別式Dの符号によって、解の個数が変わることを確認しましょう
\( {y=} \) + 1\( {x^2 } \) + 1\( {x } \) + 1
[解]
解の判別式: \(D=b^2 -4ac=\)
解の個数: 0
解: x = 0
まとめ
二次方程式の解の公式は↓のように導けます。これは二次関数の平方完成形から解いていくと導けます!
$$ \large{ x = \frac{ -b \pm \sqrt{b^2 -4ac}}{2a}} $$
そして解の個数は↓で導けます。この判別式Dは解の公式のルート内の式です。つまり、このルート部分で解が何個あるかが決まるという事ですね!
\(\Large{D=b^2 -4ac}\) としたとき、
D < 0 ⇒ 解無し(二次関数はx軸と交わらない)
D = 0 ⇒ 解1つ(二次関数とx軸が接する)
D > 0 ⇒ 解2つ(二次関数とx軸が交わる)
- 平方完成形から解の公式が導ける
- 解の個数はルート内の式、つまり判別式Dの符号によって決まる
⇒「二次関数」カテゴリ記事一覧
その他関連カテゴリ











