積分の意味を「面積」で捉えよう!シミュレーターで理解を深めよう![数学入門]
前回の記事までで、積分の別の見方について解説しました。
今回はその考え方を使って、積分の「面積計算」という視点で見てきます!
![積分の意味を「面積」で捉えよう!シミュレーターで理解を深めよう![数学入門]](https://retu27.com/wp-content/uploads/rapture_20210506233156-500x442.jpg)
目次
前回の記事の「積分=lim Σf(x)*⊿x」の観点で見てみると、、実はf(x)面積と一致
前回の記事で、積分が↓のようなシグマで表現できることについてお話しました。
\( \displaystyle \int_α^β f(x) dx\)
\( \displaystyle = \lim_{ ⊿x \to 0 } \sum_{x=α}^β f(x)*⊿x\)
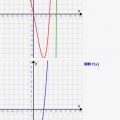
この式は細かく分割した⊿xに対して、 f(x)*⊿xを計算して合算することを意味します。これをf(x)上のグラフで図示すると、、、実は↓のようになります。
f(x)*⊿xは、グラフ上でいうと、「x地点のyと⊿xを乗算した数」であり、↑の図の緑の棒に相当します。
これを細かく分割していくと、、完全にf(x)の面積と一致しますね!つまり、↑の式の右辺はf(x)を面積を求めていることに相当するんです!

つまり、積分とは↓のような意味と捉えることが出来るんです!
\( \displaystyle \int_α^β f(x) dx\)
= f(x)のx=α~βまでの範囲の面積
マイナス面積があるときは注意
一つだけ注意点があります。それは、「関数f(x)がマイナスの領域は、マイナス面積として計算する」ということです。これも↑の式に立ち返れば当たり前のことです。
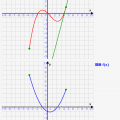
↓のような場合、x軸より下の領域の面積はマイナス扱いになり、全体から引かれます。

定積分シミュレーター!定積分のイメージを「f(x)の面積」という観点で、理解しよう!
シミュレーターの説明
上記で説明した面積計算というイメージを、シミュレーターで確認してみましょう!x=α~βの範囲を、n等分して面積計算するイメージです。関数f(x)は↓のa,b,cのパラメタを指定できます。
の各パラメタa~cを↓のスライドバーで変更すると、それを積分して原始関数F(x)が計算されます。また、シミュレーター上でそのF(x)の形状がグラフ化され、定積分の値が出力されます。
今回はそれと同時に、x=α~β区間をn等分して、面積計算した結果も表示します。実際の積分値と、面積の値との誤差が、nが大きくなるほど小さくなることを確認しましょう!
定積分シミュレーター
↓のスライドバーでf(x)の関数や、積分区間α~βを調整した後、分割数nの値を上げてみましょう!
\( {f(x)=} \) + 1\( {x^2 } \) + 1\( {x } \) + 1
\( {F(x)=} \) + 1\( {x^3 } \) + 1\( {x^2 } \) + 1\( {x } \) +C
↓nが大きくなるほど、積分値(上)と面積が近くなることを確認しましょう!
= 0.0
まとめ:積分をすると、f(x)の面積が求められる!これは重要!
上記の通り、積分をするということは、「f(x)の面積を求める」ことに相当します。これはすごく便利なことです!
例えば、↓のように複雑な関数があったときに、この面積を計算するのにはすごく大変です。しかし、積分をすると、この面積が一発で求められるんです!
この積分による面積計算は頻出する要素なので、↑のシミュレーターで理解を深めてもらえればと思います!
⇒「積分」カテゴリ記事一覧
その他関連カテゴリ