不定積分と定積分をシミュレーターで理解しよう![数学入門]
前回の記事までで、積分の基本的な考え方について説明しました。実際に積分はどうやって演算するかも、コチラの記事で解説しています
今回は、「不定積分」「定積分」について解説していきます。積分といっても、2つの種類があるんです。今回はこの2つの差について解説します。
![不定積分と定積分をシミュレーターで理解しよう![数学入門]](https://retu27.com/wp-content/uploads/20210820001629-322x500.png)
目次
普通に積分すると「不定積分」になってしまう
まずは不定積分についてです。関数f(x)に対して、それを積分演算した原始関数F(x)を求めることです。微分の逆演算をすることです。
今まで解説したとおり、完全に原始関数F(x)を復元出来るわけではないんです。それは、↓のように「微分すると定数の情報は消失する」からです。定数の微分は0だからです。
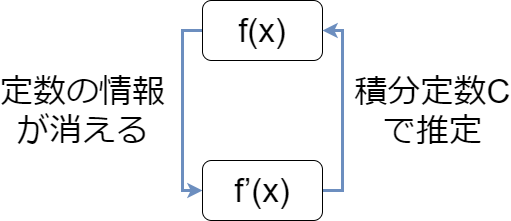
例えば、関数がf(x)=2x+2であってもf(x)=2x+3であっても微分f'(x)=2となり、定数が何だったのか分からなくなるんです!この関数f'(x)を積分するとf(x)=2x + Cとなります。定数が不明のため、不明な要素を積分定数Cとして表すんです。
これは微分・積分の意味を考えても当たり前です。微分はその関数の変化(傾き)を表す導関数を求める演算です。なので定数は消えてしまうんですね、、、><
これが普通の「不定積分」です。
区間を明示すると「定積分」になり、不明項(積分定数)が消える!
これに対して、定積分は「どこからどこまで積分するか区間を明示する」ものです。不定積分は、積分して原始関数を推定して終わりですが、定積分はそこから「区間を定めて、その区間でのF(x)の変動値を求める」という演算をします。
例えば、
という関数があったら、↓のように積分できます。
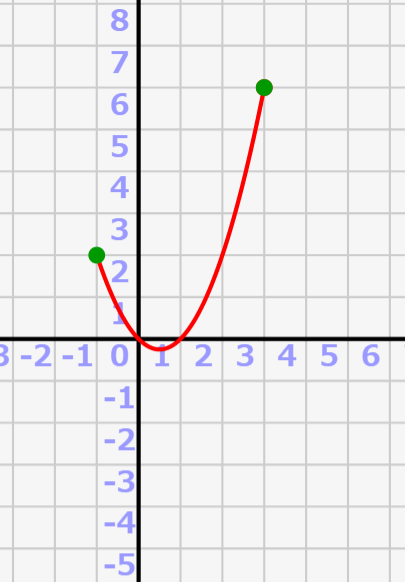
この積分後のF(x)に対して、例えばx=-1~3の区間で定積分すると決めます。この区間でのF(x)の変動値を求めえればいいので、↓のように原始関数F(x)でx=-1のときとx=3のときの差分を取ります。
これに\(F(x) = x^2 -x + C\)を適応すると、
\( = 9 -3 -1 -1 +C -C \)
\( = 4 \)
となります。4という具体的な解に定まりました!これは積分定数Cが差分をとることで打ち消し合うからです!積分をしただけだと、不明な定数Cが残ってしまうんですが、差分をとることで消えるんです。
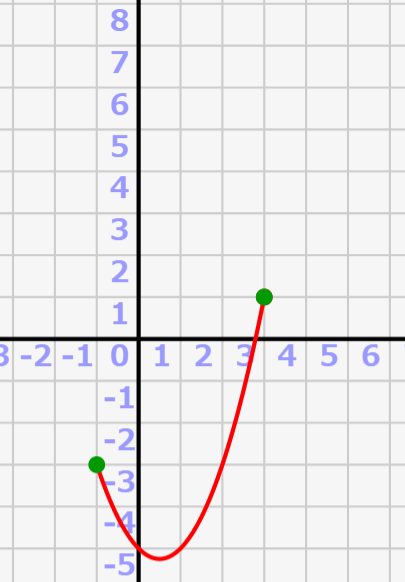
これは図で見ると一目瞭然です。
積分定数Cを変えると、F(x)の縦位置がズレます。しかし、定積分で求めているのはx=-1のときとx=3の時のF(x)の差分なので、F(x)全体で縦に位置がズレても関係ないんです! 積分定数Cが何であれ、その差は4になるわけです。
このように区間を決めて、その間での変動を求めたい場合は、定積分で具体的な解を求められるのです!
このような区間を決めて積分する定積分は、↓のような\( \int_a^b \)という記号を使って表現します。
a~bの間のf(x)の定積分= \( \int_a^b f(x) dx = F(b) – F(a)\)
定積分シミュレーター!定積分のイメージを理解しよう!
上記で説明した定積分をシミュレーターを用いて確かめてみましょう!
の各パラメタa~cを↓のスライドバーで変更すると、それに合わせて原始関数F(x)が計算されます。また、シミュレーター上でそのF(x)の形状がグラフ化され、定積分の値が出力されます。
定積分がどのように計算されるか、シミュレーターを用いて確認して見ましょう!また積分定数Cを変えても、定積分の値は全く変わらないことを確認しましょう!
\( {f(x)=} \) + 1\( {x^2 } \) + 1\( {x } \) + 1
\( {F(x)=} \) + 1\( {x^3 } \) + 1\( {x^2 } \) + 1\( {x } \) +C
= 0.0 – (0.0) = 0.0
↓値を変えると、自動的にアニメーションが始まります!
↑動的に再生速度を変えられます。左端で0にすると、一時停止となります。
まとめ:積分は不定だけど、定積分すると具体的な値が求められる!
最後にまとめです。今まで説明してきた積分については、積分定数Cが必ずついていました。それは、原始関数F(x)を推定するときに、定数項がどうしても不定となってしまうからです。
これに対して、定積分は「積分する区間を定めてF(x)の差分をとる」ことをします。この演算の場合は差分をとるので、不定項である積分定数Cが消えて、具体的な値が定まります!
この定積分は↓のような形で表記します。
a~bの間のf(x)の定積分= \( \int_a^b f(x) dx = F(b) – F(a)\)
次回の記事では、物理の「位置、速度、加速度」の例を用いて積分の有効性を説明していきます!
⇒「積分」カテゴリ記事一覧
その他関連カテゴリ