物理入門:「等加速度運動」の公式をシミュレーターを用いて理解しよう!
前回までの記事で、等速運動について学びました。今回は、その発展で「等加速度運動」について学んでいきます!等加速度運動の公式をシミュレーターを用いて解説していきます!

目次
等加速度運動の定義
等加速度運動は以下のような運動のことを言います。
加速度が一定となる運動
加速度が、時間が経過しても一定となるのが等加速度運動です。加速度が一定なので、速度は時間が経つごとに↓のように増加していきます。
\(v \displaystyle= v_0 + a_0*t \)
- \(x_0\) : 初期位置[\(m\)]
- \(v_0\) : 初期速度[\(m\)]
- \(t\) : 時間[\(s\)]
1秒ごとに加速度だけ速度が加算されるため、↑のような式になります。時間が経つと、直線的に速度が上昇していくわけですね。
この公式、何かに似ていますよね。実は、等速運動の位置を求める公式と全く同じ形をしています。ここからも、「速度→位置」の関係は「加速度→速度」の関係と同じことが分かります。
等加速度運動の公式
等加速度運動の場合、↓の式で位置xが計算可能です。
\(x \displaystyle= x_0 + v_0*t + \frac{1}{2}a_0*t^2 \)
- \(x_0\) : 初期位置[\(m\)]
- \(v_0\) : 初期速度[\(m\)]
- \(v_0\) : 加速度[\(m/s^2\)]
- \(t\) : 時間[\(s\)]
↑とは違ってやや難しい式となっていますね。これについては、↓のシミュレーターを用いてこうなる理由を説明していきます!
シミュレーターで「等加速度運動」の意味を理解しよう!
それでは上記の式の意味を、シミュレーターを使って確認してみましょう!
初速,加速度をスライドバーで設定して、実行を押すとボールが等速運動で動き始めます。
↓グラフで位置,速度,加速度がリアルタイムで表示されるので、どのような変化をするか確認してみましょう。
(↓の再生速度で時間の経過を遅くしたり、早くした理出来ます)
グラフ表示項目位置 速度 加速度
「等加速度運動」に関する重要なポイント
上のシミュレーターを使うと、等速運動と同様に以下のようなことが分かります!
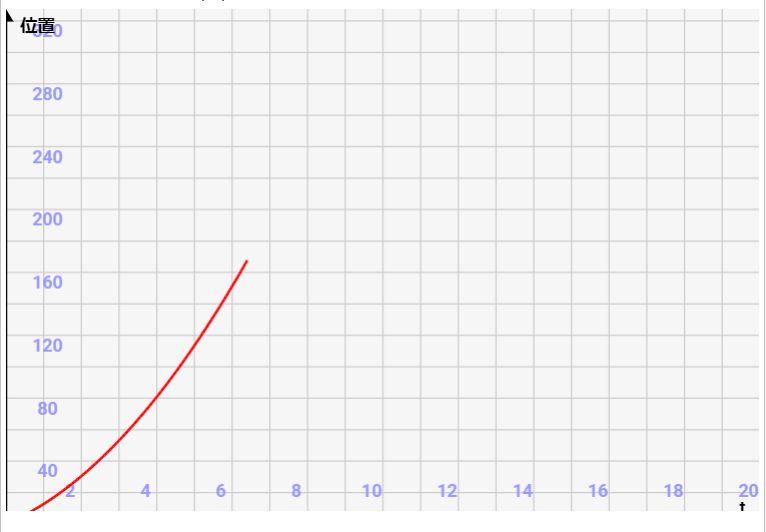
重要ポイント1:等加速度運動では、位置は二次曲線のように増加していく
これは↓の公式から当たり前ですね。\(t^2\)の項があるので、ボールの位置は二次曲線のように加速度的に変化していきます。
重要ポイント2:加速度グラフで増加した面積だけ、速度は変動する!
前回の記事で説明したのと同様ですが「加速度グラフの増加面積=速度の変動」という関係にあります。実際のシミュレーターの例で確認してみましょう!
以下、初速=10,加速度=5での例になります。
↓例えば6秒経過後には加速度グラフは↓のように5×6=30の面積になっています。
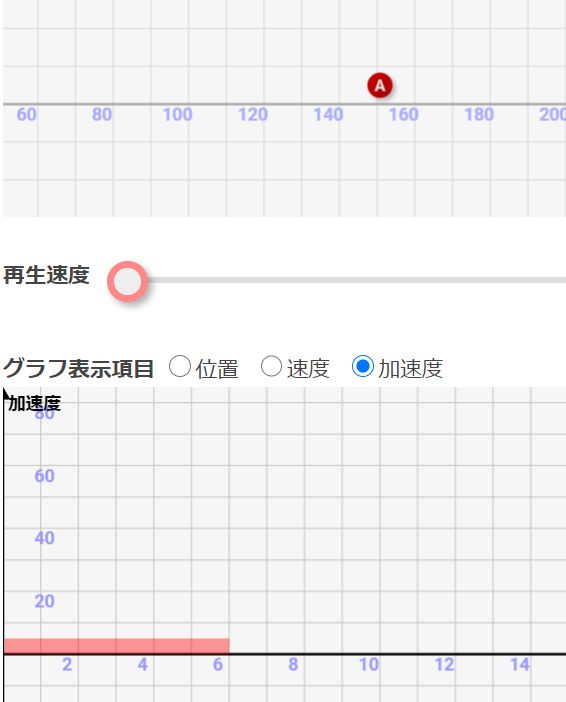
そして↓がそのときの速度です。初速が10m/sから、40m/sに加速していますね。その差は30です。加速度グラフが描いた面積分、速度が加速している事がわかりますね!
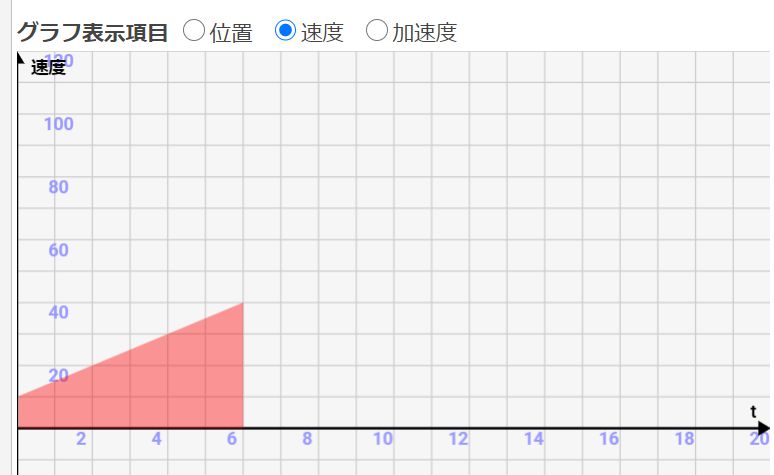
重要ポイント3:速度グラフの増加面積=位置の変動
これは、前回の記事で説明した法則になります。等加速度運動時も、同様に「速度グラフの増加面積=位置の変動」という関係が成り立ちます。
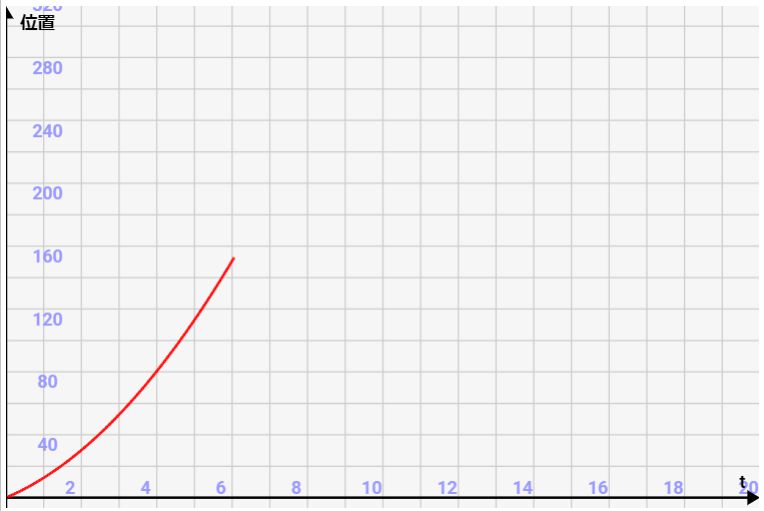
初速=10,加速度=5でt=6のときを考えてみます。
速度グラフの面積は↓のようになります。今回の場合加速しているので、台形のような形になります。台形の公式から、面積を計算すると、\(\frac{(10+40)*6}{2}\)=150となります。

このときの位置を確認してみると、、、、ちょうど150mの位置にありますね!シミュレーターからも「速度グラフの増加面積=位置の変動」となっている事が分かります!
台形の公式から、等加速度運動時の位置の公式を求めてみる!
上記の通り、「速度グラフの増加面積=位置の変動」の関係にあります。そして、等加速度運動時には速度は直線的に伸びるため↓のようなグラフになります。
ちょうど台形になっていますね。ですので、この台形の面積さえわかれば、位置(変位)が計算出来るのです!
台形の左側の辺は「初速\(v_0\)」と一致しているはずであり、右側の辺は「時刻tの速度 = \(v_0+t*a_0\)」となっています。ですので、
\(= (v_0 + v_0 +t*a_0)*t/2\)
\(= v_0 + \frac{1}{2}a_0*t^2 \)
となります。これはt=0からの移動距離であるため、初期位置\(x_0\)を足すことで
と位置が求められます。これは↑で紹介した等加速度運動の公式になります!このように、速度の面積から計算すると、この公式が導けるのです!
まとめ:等加速度運動は二次曲線的に位置が変化していく!
最後に軽くまとめです。ここまで解説したとおり、等加速度運動には、以下の式t秒後の位置を求めることができます。
\(x \displaystyle= x_0 + v_0*t + \frac{1}{2}a_0*t^2 \)
- \(x_0\) : 初期位置[\(m\)]
- \(v_0\) : 初期速度[\(m\)]
- \(v_0\) : 加速度[\(m/s^2\)]
- \(t\) : 時間[\(s\)]
等速運動時と違って、少し複雑ですね。等加速度運動だと、「加速度→速度」、「速度→位置」と二段階で影響してくるため、少し複雑になるんですね。
そんな時でも、今回解説したように「速度グラフの増加面積=位置の変動」の法則を使うことで、時刻tでの位置を求めることが可能です。
次回からは、この等加速度運動の例である物体の落下運動について説明していきます!
- 等加速度運動の位置は二次関数で表せ、速度グラフの面積(台形)からも求められる
⇒「速度・加速度」カテゴリ記事一覧
その他関連カテゴリ