物理入門:「斜方投射」をシミュレーターで理解しよう!
前回までの記事で解説した等加速度運動の例として、「斜方投射」をシミュレーターで動かしてみましょう!
地球にあるものには重力加速度g=9.8m/s^2が下方向に働いています。この重力により、ボールがどのような速度で落ちていくか、シミュレーターを用いて確認してみましょう!
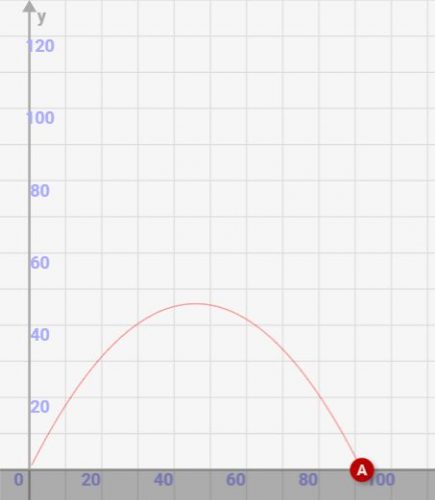
斜方投射シミュレーター
さっそくシミュレーターで実験してみましょう!
- 実行ボタンを押すと、初速x,初速yで、斜め方向にボールが投げ出されます
- スライドバーで初速x,yを自由に変えられます
- グラフ表示項目を選択すると、x,yそれぞれの位置/速度/加速度をリアルタイムにグラフ化して表示します
色々な方向にボールを投射させて、実験してみましょう!
飛距離 : 0.0 m
グラフ表示項目位置
速度
加速度
xを赤色,yを赤色で示しています
シミュレーター結果解説
以下、シミュレーターの結果を解説していきます。基本的に、落下運動は加速度運動ですので公式に当てはめれば速度/位置等が求められます。
この時のコツはx方向(横)とy方向(縦)成分に完全に分けて計算するということです。
速度の変化
x方向とy方向で分けて考えます。
y方向の速度
y方向は最初上向きの初速で飛び出しますが、重力加速度-gがかかるため、↓の式のように少しずつ遅くなり、最終的にはマイナス速度になります。
\(v_y \displaystyle= v_{y0} -gt \)
- \(v_{y0}\) : 鉛直方向初期速度[\(m/s\)]
- \(g\) : 重力加速度[\(m/s^2\)]
- \(t\) : 時間[\(s\)]
x方向の速度
x方向には何も力がかかりません。ですので、x方向は↓のように初速から変わらず、等速運動していきます。これは水平投射と同じです。
\(v_x \displaystyle= v_{x0} \)
- \(v_{x0}\) : 水平方向初期速度[\(m/s\)]
↓x方向を赤字、y方向を青字で示した速度変化です。x方向は一定の速度です。y方向は最初は30km/sからはじまり、最後落下する時には-30km/sにまでマイナス加速しています。最初と最後の速度が真逆になっているというのがポイントです!
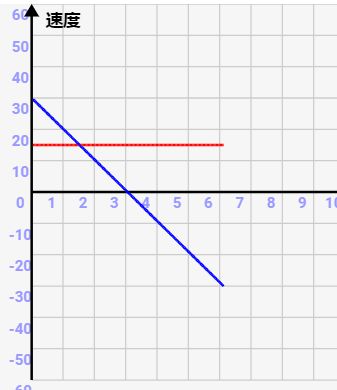
位置の変化
y方向の位置
斜方投射時の位置は、等加速度の位置公式から↓のように求められます。
\(y \displaystyle= v_{y0} t – \frac{1}{2}gt^2 \)
- \(v_{y0}\) : 鉛直方向初期速度[\(m/s\)]
- \(g\) : 重力加速度[\(m/s^2\)]
- \(t\) : 時間[\(s\)]
x方向の位置
x方向は等速運動なので、↓のようになります。簡単ですね。
\(x \displaystyle= v_{x0} t \)
- \(v_{x0}\) : 鉛直方向初期速度[\(m/s\)]
- \(t\) : 時間[\(s\)]
↓結果的に、x方向とy方向は↓のような変化になります。xは直線的に増加していき、yは二次曲線のように放物線を描きます。頂点を境目に左右の軌跡が完全に対称となっているのがポイントです!
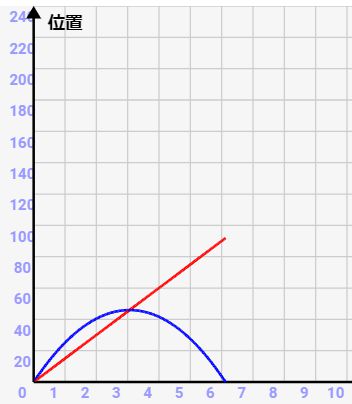
頂点到達時間
ボールが一番上になった時、ボールは\(v_y=0\)になるはずです。その地点で速度がプラス→マイナスに変わるからです。
ですので、上記で説明した\(v_y\)の式を使うと
\(t \displaystyle= \frac{v_{y0}}{g} \)
と簡単に頂点到達時間が求められます。
地面到達時間
地面到達時間は↑の位置の式にy=0を代入すれば簡単に求められます。
\( 0 \displaystyle= v_{y0} t – \frac{1}{2}gt^2 \)
\( 0 \displaystyle= t(v_{y0} – \frac{1}{2}gt) \)
\( t \displaystyle= \frac{2 v_{y0}}{g}\)
- \(v_{y0}\) : 鉛直方向初期速度[\(m/s\)]
- \(g\) : 重力加速度[\(m/s^2\)]
これは、頂点到達時間のちょうど二倍になっていますね。これはつまり「頂点に到達するまでの時間=頂点から地面に向かうまでの時間」となっている事を示しています!
↓の青線のように速度が\(v_y=0\)の頂点を中心に左右対称となっています。同じスピードで進んでいるので、最終的に同じだけ時間がかかるわけです。

到達位置(飛距離)
x方向の到達位置(飛距離)を求めるのは簡単です。地面への到達時間は↑のように求まっているので、これを\(x= v_x t\)の式に代入すればいいだけです。
\(x \displaystyle = v_x t \)
\( \displaystyle = \frac{2 v_{y0} v_{x0}}{g} \)
- \(v_{y0}\) : 鉛直方向初期速度[\(m/s\)]
- \(v_{x0}\) : 水平方向初期速度[\(m/s\)]
- \(g\) : 重力加速度[\(m/s^2\)]
シミュレーターで高さや初速を変えて実験してみて、このような到達位置になることを確かめてみて下さい!
- 頂点に到達するまでの時間=頂点から地面に向かうまでの時間
- 頂点到達時間を中心に、鉛直方向の速度はプラス・マイナス逆転する
⇒「重力・落下運動」カテゴリ記事一覧
その他関連カテゴリ














