物理入門:「鉛直投げ上げ」をシミュレーターで理解しよう!
前回までの記事で解説した等加速度運動の例として、「鉛直投げ上げ運動」をシミュレーターで動かしてみましょう!
地球にあるものには重力加速度g=9.8\(m/s^2\)が下方向に働いています。この重力により、ボールがどのような速度で落ちていくか、シミュレーターを用いて確認してみましょう!
鉛直投げ上げ運動 シミュレーター
さっそくシミュレーターで実験してみましょう!
- 実行ボタンを押すと、設定した初期y,初速yに従ってボールが上に投げられ
- スライドバーで初期y,初速vを自由に変えられます
- グラフ表示項目を選択すると、x,yそれぞれの位置/速度/加速度をリアルタイムにグラフ化して表示します
。
色々な高さや速度で投げ上げてみて、実験してみましょう!
グラフ表示項目位置
速度
加速度
xを赤色,yを赤色で示しています
シミュレーター結果解説
以下、シミュレーターの結果を解説していきます。基本的に、落下運動は等加速度運動ですので、公式に当てはめれば速度/位置等が求められます。
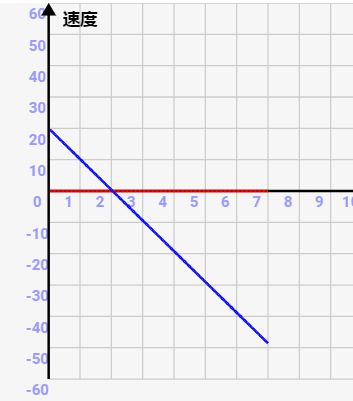
速度の変化
下方向の速度は、等加速度運動なので↓のように時間に比例して大きくなっていきます。加速度は重力加速度-gになります。
重力は高さyとは逆方向にかかるので、-gの加速度になることに注意して下さい。
\(v \displaystyle= v_0 -gt \)
- \(v_0\) : 初期速度[\(m/s\)]
- \(t\) : 時間[\(s\)]
- \(g\) : 重力加速度[\(m/s^2\)]
初速が\(v_0\)なので、途中までは速度がプラス(上方向)ですが、途中から速度がマイナス(下方向)になっていきます。
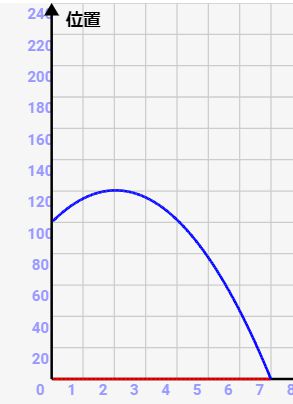
位置の変化
鉛直投げ上げ時の位置は、等加速度の位置公式から↓のように求められます。
\(y \displaystyle= y_0 + v_0t – \frac{1}{2}gt^2 \)
- \(y_0\) : 初期位置[\(m\)]
- \(v_0\) : 初期速度[\(m/s\)]
- \(t\) : 時間[\(s\)]
- \(g\) : 重力加速度[\(m/s^2\)]
つまり、鉛直投げ上げ運動ではボールの位置は↓のように二次関数状に変化するんですね。

地面到達時間
地面到達時間は↑の式にy=0を代入すれば求められます。
\( gt^2 -2 v_0 t – y_0 = 0 \)
↓二次関数の解の公式
\( t \displaystyle= \frac{2v_0 + \sqrt{4 v_0^2 + 8 g y_0}}{2g} \)
少し複雑ですが、ボールを投げおろす位置\(y_0\)に対して、落ちるまでにかかる時間tはそのルートに比例して大きくなるわけです。
しかし、上に投げる速度\(v_0\)によって、比例的に落ちるまでにかかる時間が伸びます。
このように式を解くことで、各要素がどれぐらい落ちるまでの時間に影響を与えるかが計算できるわけです!
- 鉛直投げ上げは、自由運動に上方向への投げ上げ運動が入り、複雑になる
- 速度はプラスからマイナスに転換していく
- 鉛直方向に位置は放物線を描くような形となる
⇒「重力・落下運動」カテゴリ記事一覧
その他関連カテゴリ