「三角形の面積(底辺×高さ÷2)」をシミュレーションで復習しよう![数学入門]
目次
「三角形の面積(底辺×高さ÷2)」はなぜ成り立つ?
三角形の面積は「底辺×高さ÷2」。これは小学校で習う公式で、当たり前のように使ってます。
今回はこの公式の意味ついて振り返り、この式が成り立つことをシミュレーターで確認していこうと思います!是非、この機会に復習してみましょう!
![「三角形の面積(底辺×高さ÷2)」をシミュレーションで復習しよう![数学入門]](https://retu27.com/wp-content/uploads/rapture_20201214220645-500x230.jpg)
三角形の面積の公式の確認
ここで、三角形の面積に関する公式の確認をしておきます。
\( \displaystyle 三角形の面積 = 底辺の長さ × 高さ ÷ 2 \)
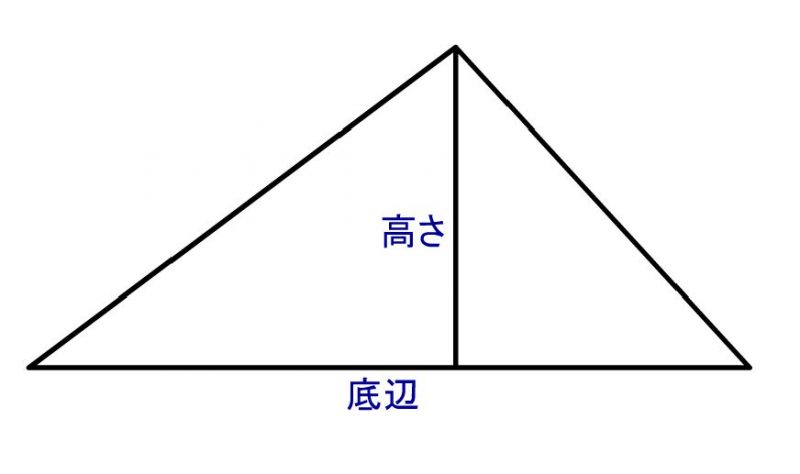
この中で「底辺」と「高さ」は↓の部分のことを示しています。底辺は下となる辺のことで、「高さ」はその底辺から頂点までの距離のことをいいます。
つまり、底辺と高さが分かれば面積は計算できます。「どんな形の三角形であっても、底辺と高さが同じなら面積は同じ」というとこがポイントです!
三角形の面積が「底辺×高さ÷2」となる理由
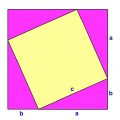
「底辺×高さ÷2」となるのは↓のような図を書いてみればすぐに分かります。
当然ですが、この図の長方形全体の面積は「横(底辺)×縦(高さ)」です。そしてその中に三角形(紫色)が入っていますが、よくみるとその他の領域(緑色部分)も同じ面積を持っていることが分かります。
つまり、「三角形の面積×2 = 長方形の面積」となるため、三角形の面積は「底辺×高さ÷2」となるわけです!
三角形の面積の変化をシミュレーターで実験して理解しよう!
上記の公式の通りに三角形の面積が計算できるのか、実際にシミュレーターでその動きを確かめてみましょう!
↓の値を変えると、三角形の「底辺」「高さ」「頂点の位置」を変更できます。頂点の位置を変更すると、頂点を左右に移動できます。これらの値を変化させて、本当に三角形の面積が「底辺×高さ÷2」になるのか確認して見ましょう!
三角形の面積は「底辺×高さ÷2」であり、頂点がいくら移動しても面積は変化しない!
↑のシミュレーターでポイントとなるのは「面積は底辺と高さのみで決まる」という事です。ですので、高さが変わらなければ、頂点がどこにあっても面積は一切変わりません。
そのため、↓の3つは全て同じ面積になります。
全く違う形をしていますが、全て同じ面積です。頂点の位置により、三角形がすごく傾いたりしますが、どれだけ歪んでも高さが変わらなければ面積は同じということを意識しましょう!
次回は直角三角形の公式について確認していきます!
今回は、小学校で習う三角形の面積の公式「底辺×高さ÷2」をシミュレーターで復習してみました!簡単な話ですが、どんな分野でも普通に使われるところなので><
次回は今回作ったような直角三角形の重要な公式について解説します!
- 三角形は2つ合わせると長方形になるので、長方形÷2が三角形の面積となる
- 底辺と高さが同じなら、全て同じ面積となる
⇒「幾何学・図形」カテゴリ記事一覧
その他関連カテゴリ