「三平方の定理」をシミュレーションで復習しよう![数学入門]
目次
三平方の定理について解説します!
今回は三平方の定理について解説します。三平方の定理は直角三角形を考える時に非常に重要となる定理です!
様々な分野で出てくる重要な定理ですので、シミュレーターを使ってその意味を理解しましょう!証明についても解説していますよ!
三平方の定理
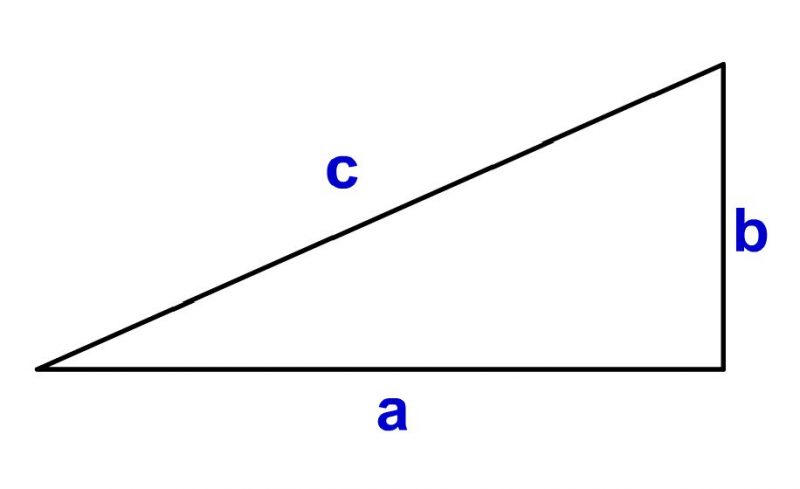
↓のような直角三角形を考えます。↓のように底辺をa,高さをb、斜辺をcとします。
このときにa,b,cの間には↓のような関係性があります。これを三平方の定理といいます。
直角三角形の斜辺cとその他二辺a,b(↓のような直角三角形)において、以下の式が必ず成り立つ
\( \displaystyle c^2 = a^2 + b^2 \)
この式からcについて求めると、
直角三角形で底辺がa,高さがbであれば斜辺の長さは以下の値となる。
\( \displaystyle c = \sqrt{a^2 + b^2} \)
という式になります。
三平方の定理の重要な意味
上記の式は、直角三角形なら二辺さえわかれば、もう一辺は計算できるということを意味しています。
特に、底辺と高ささえわかれば、斜辺はすぐに計算できますし、斜辺と底辺がわかれば高さもすぐに分かります。数学や物理等で色んな場面で現れる重要な公式です!
三平方の定理の証明
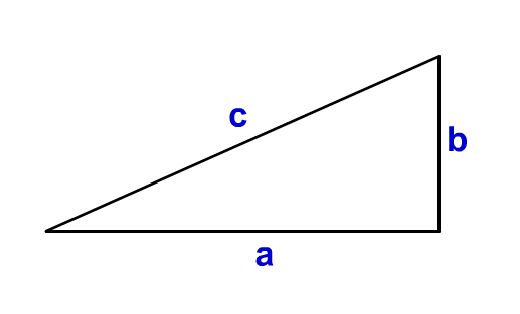
この三平方の定理は以下のようにして証明できます。↓のような三角形があるとして、、、。
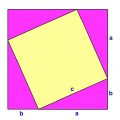
↓のように三角形を並べた状況を考えます。4つ同じ三角形を並べて、真ん中に四角形を作ります。
詳しく描くと↓のような感じ。真中の四角形の周りの4つ同じ三角形を配置します。
すると、この四角全体は一辺が(a+b)なので、
となります。さらに、黄色の四角についてみると、一辺がcなので
となります。そして、三角形の面積はもちろん
ですね。そしてこれらの面積の関係は図を見れば分かる通り、↓のようになります。
なので、上記の式をこの式に代入して計算すると、、、
↓展開
\( \displaystyle a^2 + b^2 + 2 a b = c^2 + 2 a b \)
↓両辺から2abを消去
\( \displaystyle a^2 + b^2= c^2 \)
となり、上記の公式が証明できます!ちょっとテクニカルですが、上記の式は直角三角形で常に成り立つ定理になります!
三平方の定理をシミュレーターで理解しよう!
それでは上記で示した三平方の定理を、シミュレーターで確認してみましょう!
↓の値を変えると、三角形の「底辺」「高さ」を変更できます。これらの値を変化させて、斜辺の長さがどう変わるか確認してみましょう!!
二辺から三辺が求められれば、cosθやsinθも計算可能に!
上記のように、直角三角形のときには二辺が分かっていれば、3辺目も求めることができます。
すると、コチラのページで詳しく解説している通り、cosθとsinθもすぐに求められます。
cosθ=「斜辺と角θをなす横辺(赤線)」の長さ/斜辺の長さ(黒線)
sinθ=「角θと接さない縦辺」の長さ(青線)/斜辺の長さ(黒線)
↓この絵の角度θについて、cosθとsinθが簡単に求められるんです

ですので、結局、2辺が求められれば、全てが求められてしまうのです!便利ですね!
- 「三平方の定理」は図形を考える時に使う最重要な定理
- ↑で描いたような対象三角形と四角形を組み合わせた図で成り立つことが示せる
⇒「幾何学・図形」カテゴリ記事一覧
その他関連カテゴリ