度数分布表/階級をシミュレーターで理解しよう![統計学/確率入門]
本サイトでは、数学分野の内容を基礎から分かりやすくシミュレーターを用いて解説しています!このベースを用いて、以後「統計学/確率」の分野の内容を同様にシミュレーターを作って解説していきたいと思います!
前回までに「平均」「中央値」「分散」などの代表値の解説をしてきました。そこでは、↓の図のようなグラフを用いてきました。このようなグラフですが、もう一つ重要な見方があります。それは「結局どの辺りの点数が多いのか?」という観点です。
平均値なども知りたいですが、結局どの辺りに点数が多いかというのは重要な情報であり、その分布を見るのは統計を扱う上で大事な要素です。
今回はそのようなグラフ(ヒストグラム)を作るための、度数分布表/階級の作り方を説明していきます!シミュレーターもあるので、是非実験して理解しましょう!
![度数分布表/階級をシミュレーターで理解しよう![統計学/確率入門]](https://retu27.com/wp-content/uploads/rapture_20200707001458-500x483.jpg)
目次
度数分布表とは
今回もテストの0点~100点のテストの点数を例として説明していきます。今回はn=50人のクラスでテストを行った時のデータを例題にして考えていきます。
いきなりですが、分布表の例を↓に示します。コチラが分布表です。
| 階級 | 階級値 | 度数 | 相対度数 |
|---|---|---|---|
| 0 ~ 10 | 5 | 1 | 0.02 |
| 10 ~ 20 | 15 | 2 | 0.04 |
| 20 ~ 30 | 25 | 5 | 0.1 |
| 30 ~ 40 | 35 | 8 | 0.16 |
| 40 ~ 50 | 45 | 8 | 0.16 |
| 50 ~ 60 | 55 | 15 | 0.3 |
| 60 ~ 70 | 65 | 7 | 0.14 |
| 70 ~ 80 | 75 | 1 | 0.02 |
| 80 ~ 90 | 85 | 3 | 0.06 |
| 90 ~ 100 | 95 | 0 | 0 |
この分布表は、一番左列の階級ごとに、どれぐらいの人数が分布しているかを示した表です。不明な用語多いので、以下詳しく解説していきます!
用語の説明
上記の度数分布表の各列の意味は以下のとおりです。
階級
階級は上の表でいう「○○以上xx未満」という部分のことです。例えば「10 ~ 20」は「10以上20未満の区分」という意味です。度数分布表では、階級によって各段階に一定間隔にデータを区切ります。その下限と上限を示す「xx以上xx未満」という部分を階級といいます。
度数
度数は「○人がその階級に属しているか」という情報です。10点以上20点未満の人が3人いた場合、「度数=3」です。簡単ですね!
階級値
階級値は「その階級を代表する値」のことを言います。簡単にいうと、その階級の中心の値です。「10以上20未満」の階級であれば、\(\frac{10+20}{2} = 15\)が階級値になります!
相対度数
相対度数は「全体のうちどれぐらいの割合の人がその階級にいるか」を表した数字です。例えば、50人のクラスで、「40以上50未満」の階級に10人が属していた場合、「相対度数\(=\frac{10}{50}=0.2\)」になります。つまり、クラスの20%がこの階級に属しているという意味です!相対度数は全体を1とするので、20%なら0.2、15%なら0.15になることに注意して下さい。
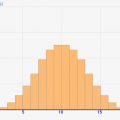
上記の度数分布表は、↓のようなグラフ分布になります。縦軸が度数(その区分の点数にあてはまる人数)です。このグラフをヒストグラムといいます!このようにヒストグラムにすると、どの辺りにどれぐらいの人数がいるかが分かり、非常にデータが分かりやすくなります!
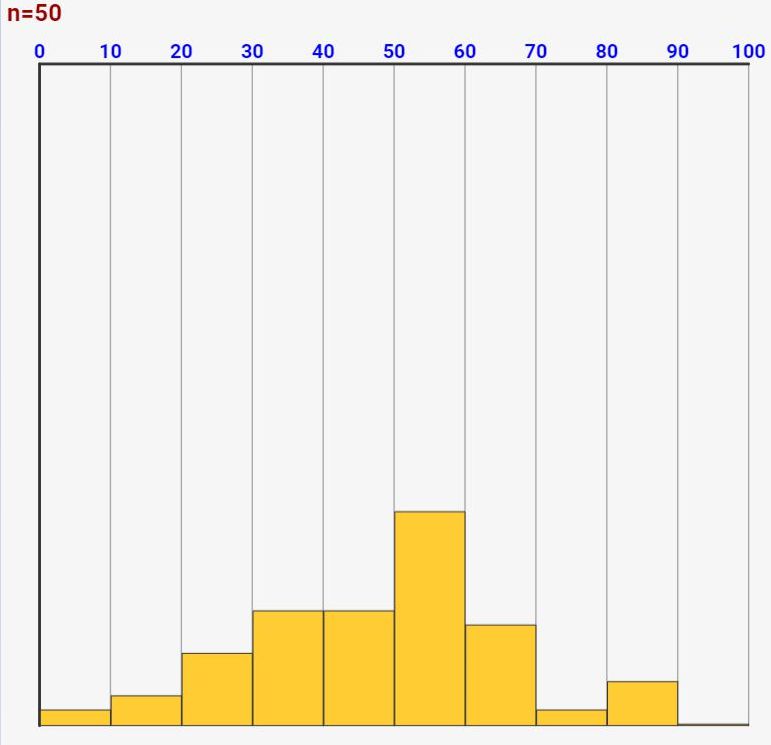
度数分布を使うと、データの分布が分かりやすくなるわけです!
度数分布表/階級シミュレーターでイメージを掴もう!
上記のような度数分布表の理解を深めるため、度数分布表/階級シミュレーターを作ってみました!
- このシミュレーターでは予め点数分布データを作成しており、それ自体は変わりません
- しかし、↓のスライドバーを動かすと、階級の幅(1階級区分の幅)を変えられます
- シミュレーターは分布が終わると、ヒストグラムと度数分布表を作成していきます
- 再分布ボタンを押すと、点数分布も再びランダムに配置し直すことができます
色々区分を変えてみて、区分によってヒストグラムの形や分布表が変わることを確認してみましょう!
作成された度数分布表
度数分布表から簡易に平均値を計算してみよう!
↑のシミュレーターのように、度数分布表は「ざっくりどれぐらいで点数が分布しているか示す表」です。この表から平均値を計算することを考えてみましょう。
まず、度数分布表にまとめた時点で細かい情報が欠けてしまったので、あくまでざっくりとしか計算できません。その前提のうえでですが、以下のような計算法で平均値をざっくり計算することが可能です!
おさらい:平均値の定義
まず平均値の計算方法のおさらいです。詳細はコチラの記事で解説していますが、
\(x_i\): i番目の人の点数
という表記を前提として、↓の式で計算できます。
\( 平均値 \)
\( \displaystyle = \frac{1}{n}(x_1 + x_2 + … + x_n) \)
\( \displaystyle = \frac{1}{n}\sum_{i=1}^{n}x_i \)
結局、「全ての点数の合計÷人数」を計算すると平均値になるわけです。
平均値の求め方1:階級値×度数を足し合わせて全体数で割る
上記のような計算方法になりますが、度数分布表では各者の点数は分からないですよね。しかし、各階級に属する人数(度数)はわかります。
そこで「各階級に属する人、平均すればざっくり真ん中の階級値になるものとして計算する」という方法をとります。つまり前後はあれど、10点以上20未満の階級の人は全員中央の15点(階級値)をとったとみなします。
すると、各階級の合計点は
\( \displaystyle = 階級値 \cdot 度数 \)
で表せます。点数×人数(度数)が合計点なので。
全合計点は
\( \displaystyle = \sum_{全階級} (階級値 \cdot 度数) \)
と表せるわけです。
そのため平均値は、全人数nを用いて
\( \displaystyle = \frac{全合計点}{全人数} \)
\( \displaystyle = \frac{\sum_{全階級} (階級値 × 度数)}{全人数n} \)
と表せます!簡単にいうと、「各階級の人の点数をざっくり階級値とみなしてしまう」というのがポイントです。もちろん、本当の平均値からは少しズレますが、大体で><
平均値の求め方2:階級値×相対度数を合算する
コチラも、考え方/本質は同じです。ただ、
になるので、実は
\( = \displaystyle \sum_{全階級}(\frac{階級値 × 度数}{全人数}) \)
\( = 「平均値の求め方1」の平均値と同じ \)
になるんです!つまり全階級の階級値×相対度数を足し合わせれば平均値になっているんです!これは便利ですね!
まとめ:度数分布表を作ると、「どの辺りの点数が一番多そうか」わかって便利です!
最後にまとめです。本記事では、度数分布表を解説をしました。
度数分布表は、「どの辺りに、どれぐらいの人数が分布しているか」を簡単に表せるように、点数を適当な区間で区切って分布を調べるものです。階級分布表では「階級」「度数」「階級値」「相対度数」などの用語が出てきますが、意味を理解すれば簡単です!
一番重要なのは、度数分布表さえつくれれば、ヒストグラムが作れるということです!ヒストグラムを見れば、各階級(点数)に属する人が何人ぐらいいるかが一目でわかります!
ヒストグラムは元データと比べて圧倒的にデータ量が少ないです。ですが、分布や平均値などざっくりとは把握できるんです。そのため、ヒストグラムは効率的なデータ圧縮ということもできます!
是非、上記のシミュレーターで度数分布表の意味を理解して、活用出来るようにしましょう!

- 度数分布 = データを区間分けして、どの区間が多いか一目で分かるようにしたもの
- 度数分布表でも大体の平均値は計算可能
- ヒストグラムを使うと、ざっくりでデータを圧縮できる
⇒「平均/分散等の代表値」カテゴリ記事一覧
その他関連カテゴリ