「原子量/相対質量」「同位体」をシミュレーターで理解しよう![化学入門]
前回記事から化学の分野についての解説をしていきます。化学で一番の基礎といえるのが「原子」です。
本記事では「原子量」「同位体」を解説していきます!
![「原子量/相対質量」「同位体」をシミュレーターで理解しよう![化学入門]](https://retu27.com/wp-content/uploads/20220430003200-475x500.png)
目次
おさらい:化学の基礎の基礎。原子とは?
原子とは、「この世界を構成する最小要素」です。地球にあるもの、宇宙にあるものの全てがこの「原子」で構成されます。
原子は↓の「陽子」「中性子」「電子」の3つで構成されます。
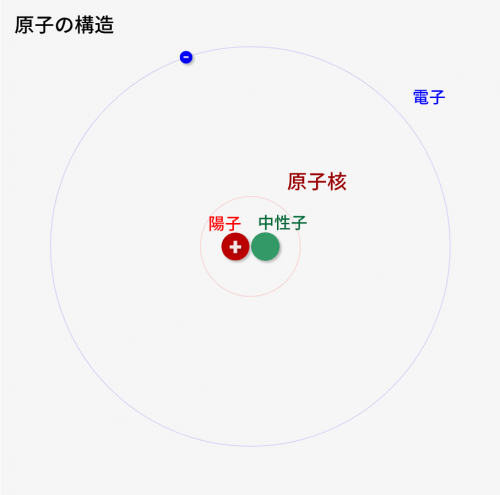
陽子
- 中性子とともに、中心(原子核)を構成する要素
- 中世子と同じ質量を持つ
- 電子とは真逆のプラスの電荷をもつ
中性子
- 陽子とともに、中心(原子核)を構成する要素
- 陽子と同じ質量を持つ
- 電荷をもたない
電子
- 原子核のまわりを回る要素
- 陽子とは真逆のマイナスの電荷を持つ
- 陽子/中性子と比べると小さく、質量がほとんどない
まとめると↓のようになります。
| 質量 | 電荷 | |
|---|---|---|
| 陽子 | +1 | +1 |
| 中性子 | +1 | 0 |
| 電子 | 0 | -1 |
*正確には電子も質量はあるが0に限りなく近い値となる
「原子量/相対質量」と「同位体」
相対質量 = \(^{12}_{6}C\)を基準にした各元素の質量
原子量は「各原子の重さを知るための基準」です。そのために、↓の「相対質量」という基準を設けます。
「\(^{12}_{6}C\)の質量 = 12」と定めたときの、各元素の質量
つまり質量数12の炭素を、12としたのですから、基本的に各元素は「質量数=相対質量」になります!例えば\(^{2}_{1}H\)は相対質量2.0になるわけです!(厳密にいうと電子の重さも入るので、微妙に誤差はでます)
↓質量数12の炭素のイメージ
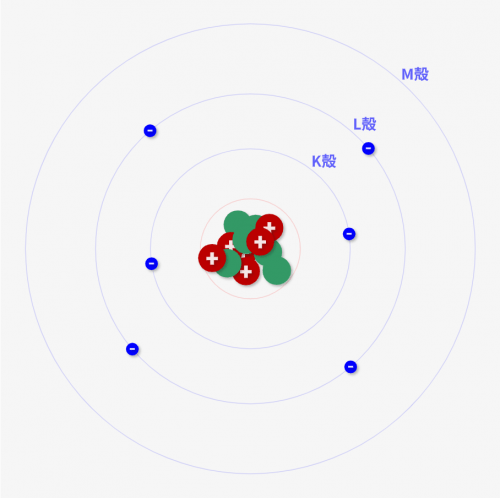
同位体 = 各元素種類で中性子数が違うものグループ
↑のように相対質量は定義できますが、実際の質量を考えるときに難しいのは、「各元素ごとで中性子数が違うものがある事」です。
例えば炭素Cでも「\(^{12}_{6}C\)」「\(^{13}_{6}C\)」の2種類が主に存在するんです。このように、同じ原子番号を持つけど、質量数が違うものを「同位体」と言います。
同じ原子番号(陽子数)をもっているけど、質量数が違うもののグループ
どのぐらい同位体があるかは、元素種別によりますし、環境にもよります。地球上では「\(^{12}_{6}C\)」「\(^{13}_{6}C\)」がほとんどなのですが、厳密には「\(^{14}_{6}C\)」「\(^{15}_{6}C\)」「\(^{16}_{6}C\)」という状態もあるんです!
原子量 = 同位体の存在比率も考慮した質量
各元素は同位体を持つので、実際に各元素の重さを考慮するときにはその存在比率を考えなければいけません。
そのため、実際に各原子番号の原子の質量を考えるときには↓の「原子量」を使用します。
各同位体の相対質量を、存在比率で平均をとった値
= \( \displaystyle \sum^{同位体} 存在比率 * 相対質量 \)
簡単な例でいうと「\(^{12}_{6}C\)」が75%、「\(^{13}_{6}C\)」が25%存在するとしたら↓計算で質量数は12.25という事になります!
「原子量」をシミュレーターで計算してみよう!
それでは、実際に存在比率を考慮した、原子量の計算をしてみましょう!今回は簡単に「水素」で考えています。
水素は一般的に「\(\large{^{1}_{1}H}\)」と「\(\large{^{2}_{1}H}\)」が天然に多く存在しています。この二つの同位体の比率を変えて実験してみましょう!
- 「\(\large{^{1}_{1}H}\)(相対質量 1.0)」と「\(\large{^{2}_{1}H}\)(相対質量 2.0)」の2種類の同位体が↓の中に表示されます
- スライドバーによって「\(\large{^{1}_{1}H}\)の存在比率」が変えられます
- 存在比率によって、水素全体の原子量がどのように変化するか確認してみましょう
赤で陽子、緑で中性子、青で電子を示しています。
参考:実際の原子量
↑のような計算で原子量を求めていくわけですが、実際の地球上での原子量は↓のようになっています(抜粋)。同位体が複数あっても、結構存在比率に偏りがあり、原子量は整数に近い数になっているのがわかると思います。
水素 1.008 \(^{1}H\):99.98%, \(^{2}H\):0.01%
炭素 12.01 \(^{12}C\):98.93%, \(^{13}C\):1.07%
窒素 14.007 \(^{14}N\):98.64%, \(^{15}N\):0.36%
酸素 15.999 \(^{16}O\):99.75%, \(^{17}O\):0.04%, \(^{18}O\):0.21%
まとめ:原子の質量は同位体を考慮して「原子量」で表す!
今回は原子の質量をどう表すかを説明しました。
基本は「\(^{12}_{6}C\)」を質量12と決めて、各原子の質量を計算していきます。
各原子ごとに中性子の数が違う同位体が存在するため、実際に使用する「原子量」は↓のように表します。
各同位体の相対質量を、存在比率で平均をとった値
= \( \displaystyle \sum^{同位体} 存在比率 * 相対質量 \)
中性子を持つ個数によって相対質量が変わるため、同位体の存在比率を考慮して地球上での原子量を計算していくわけなんです!
- 「\(^{12}_{6}C\)の質量 = 12」を基準と定め、各原子の相対質量を定義する
- 原子量は、同位体の存在比率を考慮して相対質量を足し合わせたもの
- この原子量をベースに、各原子の質量などを計算していく
⇒「元素の構成」カテゴリ記事一覧
その他関連カテゴリ