2進数とは何かをシミュレーションで解説！「繰り上がり」の動きが視覚的にわかります！[コンピューターの原理基礎]

2022-02-27　

前回に引き続いて、コンピューターの動作原理を順番に解説していきます。今回はコンピューターの計算の話をする前の、コンピューターで扱う「２進数」の数の解説をしたいと思います。コンピューターの世界では、前回の回路でも示したように１と０のみで記号化した世界です。なので、０~９まで数字のある１０進数よりも、０と１しかない２進数で計算をしたほうが都合がよいのです。

では、その２進数とは何かを今回は解説致します。もちろんシミュレーターを用いて、わかりやすく２進数とは何かを示したいと思います！

1 2進数と10進数の違いは「いつ繰り上げを行うか」のルールが違いのみ
2 2進数と10進数の繰り上がりの違いを、シミュレーターで理解しよう！
3 2進数のほうが計算パターンが圧倒的に少ない。だから、コンピューターでは2進数を使う。

2進数と10進数の違いは「いつ繰り上げを行うか」のルールが違いのみ

それでは2進数とは何かを説明していく前に、実際の10進数と2進数との対応表をまずお見せしたいと思います。

10進数	2進数
0	0
1	1
2	10
3	11
4	100
5	101
6	110
7	111
8	1000
9	1001
10	1010

どうでしょうか。2進数はなんとなく0と1しかなさそうな数であることが分かると思います。ちゃんというと、2進数とは「2以上の数になったら繰り上がりを行う、数字の表記法」です。もっと砕いていうと、「1桁に2以上の数字を入れてはいけないルール」に基づいた表記法です。

上記の例で解説します。10進数の2は2進数では10となっています。これは1+1=2となった数に対して、「2以上の数になったら繰り上げる」というルールをもとに、繰り上がりをおこなった結果です。10進数と2進数の違いは「10以上の数になったら繰り上げを行う」か「2以上の数になったら繰り上げを行う」かだけです。その他は全く変わりません。

2進数と10進数の繰り上がりの違いを、シミュレーターで理解しよう！

上記の通り、2進数と10進数の違いは「繰り上げをいつ行うかのルールが違う」だけです。その違いをわかりやすく理解するために、簡単な数をカウントしていくシミュレーターをつくりました！

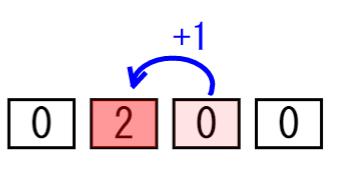
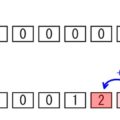
このシミュレーターでは「＋１」ボタンを押すごとに、10進数と2進数で数が1ずつ追加されていきます。各枠がそれぞれの数字のけたを表しています。ボタンをタップしてみてください！（RESETボタンで0に数字を戻します）

いかがでしょうか。シミュレーターでは計算過程を示すために、わざと下記のように数字を2以上はいるようにしています。そして、2以上の数字となった時に、繰り上がりがおこることをわかるようにしました（繰り上がりをおこした桁は、0に戻ります）。

上記のシミュレーターでみるとわかるとおり、「2進数ではその桁が2となったときに繰り上がりがおこる」のであり、「10進数ではその桁が10となった時に繰り上がりが起きる」のです。その違いは「いつ繰り上がりが起きるか」だけであり、それ以外には違いはないのです。
　

2進数のほうが計算パターンが圧倒的に少ない。だから、コンピューターでは2進数を使う。

上記のように2進数と10進数は繰り上がりのルールが違うだけで、そこまで大きな差はありません。ではなぜコンピューターは2進数を使うのかというと、「計算パターンが10進数より圧倒的に少ない」からです。

コンピューターで計算するためには、1桁ごとに計算を行う必要があるのですが…数字のパターンが大きいとそれだけ、計算を行うための計算回路が必要になってしまうんです。10進数の場合は0~9まで数字があったり、かつ繰り上がりがあったりで色んなパターンがあります。
しかし、2進数で1桁の計算パターンを見てみると…圧倒的に10進数よりパターンが少ないです。そのパターンは「0」「1」「繰り上がり」と単純にいうと３つしかないんです。ですので、この3つのパターンを扱えれば、2進数の計算はできてしまうんです。1桁ごとに計算していけばいいのですから。

ということで、次回はこの「0」「1」「繰り上がり」という3つのパターンを2進数の計算回路ではどう表現していくのかを説明していきます！
　

まとめ