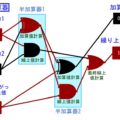
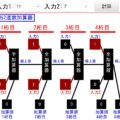
「浮動小数点」をシミュレーションで解説！[コンピューターの原理基礎]

2022-02-28　 データ型

コンピューターは2進数の世界で動いています。2進数は1001101101みたいな感じで0と1の羅列となってます。

前回、簡易的な小数点の表現方法の「固定小数点方式」について解説しました。今回はその弱点を補う「浮動小数点方式」について解説します！

おさらい：「固定小数点」

コンピューターは↓のように0 or 1が入る箱(bit)を組み合わせて、それによって数値表現をします。

↓は1バイト(8bit)で、数値としては0~255の256パターンを表現できます！

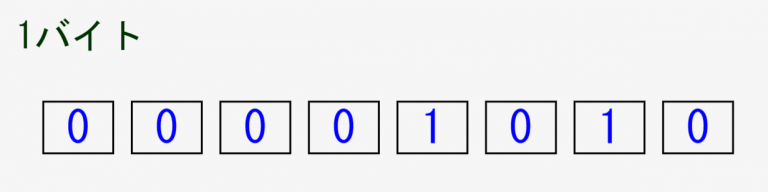
これに対して固定小数点方式は↓のように小数点の位置をどこか固定的にズラします。↓の場合は1つ左にズラした時の図です。

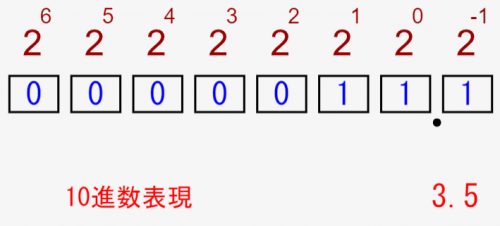
この場合、2進数で「11.1」と評価されます。
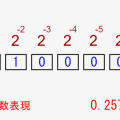
また、2進数の小数は↓のように2の累乗の逆数で評価されるので、「2進数の11.1　⇒　10進数の3.5」と評価できるんです！

ただし、固定的に小数点の位置を決めるため、「整数部分が足りなくなる」「小数部分が足りなくなる」ということが起きてしまうのです＞＜

浮動小数点 = 小数点の位置を指定できる方式

↑のような固定小数点方式の問題に対して、浮動小数点は↓のような解決法をとります！

つまり、↓のような形のデータにして、「どこに小数点を置くか」も指定できるようにしたわけです（プラスして先頭はプラスかマイナスかを示せるようになっています。

具体的な浮動小数点(2バイトの例)

それでは、具体的に浮動小数点による表す数値の決まり方と用語を見ていきます。今回は簡単のために2バイトの浮動小数点での例を見ていきます（4バイト、8バイトもありますが長くなるだけで基本的な仕組みは同じです）

浮動小数点は「符号ビット」「指数部」「仮数部」で構成される

↓が具体的な2バイトの浮動小数点の形式です。

浮動小数点は3つの場所に分かれています

符号bit

これは単純にプラスなら0、マイナスなら1とするだけです。

指数部

これは前回の固定小数点で説明していた「小数点をズラす操作」になります。ただし、決めの関係で00000と11111は使えないです(無限や0などの特殊状態を示すのに使用)。

そのため、0001～11110までの30通りで指数を示します。このときに「01111を基準点とし、↓のように仮数部の一番左にする」という決めになっています（右端基準ではない）

そして、01111以下であれば小数点を左にズラし、01111以上であれば小数点を右にズラすようにします。

↓指数部10001の例。「10001 – 01111 = 十進数で2」で、基準点から右に2つズレた位置に小数点が置かれます。

仮数部

仮数部で実際に評価される2進数を指定します。この数値は↑で定義した指数部だけズラして評価されます。

ただし、↓のような左が0で空いている状態で表現したら、もったいないですよね。だったら指数をずらして、↓の11を左にもっていったほうがより細かい数字も表現できてよいはずです。

そこで、仮数部は「一番左側に1があるとこまでズラして置く」というルールを設けて配置することになっています。

しかし！このルールなら「一番左は1しか来ないので、自明じゃないか！」ということになります。どうせ1なので、一番左のbitは無駄になります。

そこで、浮動小数では、さらにもう一段左にズラして「仮数部の左に1があるものとみなす」という前提を設けます！↓のように仮数部には数値がなくても、1があること前提になっているんです！これを「ケチ表現」といいます。

↑のように、仮数部のすぐ左に幽霊のような1がある」状態になるんです。ちょっと不思議ですが、このほうがbitを節約して細かな値を表現できるようになるんですねー

総合的に浮動小数点で表される数値

ややこしいですが、結局、↑の「符号ビット」「指数部」「仮数部」の3つで表される数値は↓のような数式で表現できます。

ちょっと難しいですよね。ということで、シミュレーターで実際の動きを確認してみましょう！

「浮動小数点」シミュレーターで理解を深めよう！

↑の解説だと難しいところありますが、、、実際手を動かして実験してみると「符号ビット」「指数部」「仮数部」が理解出来てくると思います！

符号bit 0  1 

浮動小数点シミュレーターの考察

大きな整数から小さな小数まで細かく表現が可能

固定小数点の場合、小数点の位置が固定されるため、小数か整数どちらかしか細かく表現できませんでした。

しかし、浮動小数点は指数部で自由にそこを操れるので、、、↓のように大きな数や

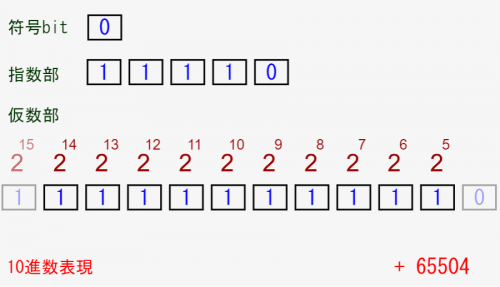
↓のような細かい数も表現できます。
↓必ず左端に1がくるため0がつくれない

2バイトなので微妙ですが、4バイトや8バイトとになるともっと巨大な数、もっと小さな数が表現可能です！

0は表現できないので、特殊記号を使う

↑の説明の通り、ケチ表現のために「仮数部の左には1がくる」という前提になっています。そのため、どう頑張っても0は表現できません！

↓必ず左端に1がくるため0がつくれない

このため仮数部＝0などとして、特殊な状態として表現する必要があるのです！
　

[関連記事] コンピューターでの小数の表し方

1．固定小数点

2．浮動小数点(本記事)