化学反応速度をシミュレーターで解説(2)![化学入門]
前回記事で、「化学反応速度」「化学平衡」について解説しました。
今回はこの化学反応速度について、もう少し複雑な場合を詳しく解説します。
![化学反応速度をシミュレーターで解説(2)![化学入門]](https://retu27.com/wp-content/uploads/20220527004237-391x500.png)
目次
おさらい:化学反応について
化学反応とは「ある分子/原子から、ある分子/原子から推移する反応」です。例えば酸素でいうと↓のように、結合されていたものが分解することも化学反応の一種です。

化学反応には「反応速度」がある
反応速度
原子/分子が化学反応で変化していくときに「化学反応速度」というものが考えれれます。
化学反応の中には一瞬で終わるものもあれば、何時間もかけて進むものもあります。
今、↓のような化学反応を考えます。AからBに変化する化学反応です。
A ⇒ B
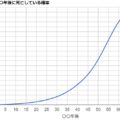
このような化学反応に対して、化学では反応速度を↓のようなグラフで表します。これは「横軸 = 時間」「縦軸 = 対象原子/分子の濃度」で表したグラフです。赤が変化前のA、青が変化後のBの濃度になります。このように少しずつAからBに変化していくわけです。

このグラフを見れば、時間あたりの反応速度が分かります。曲線の傾きが大きい最初ほど、反応速度が高いわけです。また、変化前分子と変化後分しの割合は↑のように真逆の濃度グラフになるんです。
おさらい:化学反応は、生成前分子の濃度で決まることが多い!
化学反応の速度ですが「生成前の分子の濃度」に比例することが多いです。式にすると↓のようになります。
「A ⇒ Bの反応速度」 = \(k_A[A]\)
「B ⇒ Aの反応速度」 = \(k_B[B]\)
[A]は「Aの濃度」、[B]は「Bの濃度」を表す化学の記号です。そして反応速度は↑の係数\(k_A[A]\),\(k_B[B]\)で決まるわけです。この\(k_A[A]\),\(k_B[B]\)が大きいほど素早く反応が進むわけです。また、化学平衡の条件を考えると↓のように計算ができます。
\(k_A[A]\) = \(k_B[B]\)
↓変形
\(\large \frac{[B]}{[A]}=\frac{K_A}{K_B}\)
つまり、BとAの比率は、化学反応速度係数の\(k_A\),\(k_B\)の比率で決まるわけです!
もう少し複雑な場合の化学反応式
↑ではAとBの単純な反応でしたが、実際にはもう少し複雑なが反応になります。その例が↓のような反応です。
A + B ⇒ AB
これはAとBがペアになって、ABになるという化学式です。このような式になると、反応速度は↓のように少し複雑になります(このような式にならないものも有り)
「A + B ⇒ ABの反応速度」 = \(k[A][B]\)
実は「A + B ⇒ AB」の反応速度は「Aの濃度」と「Bの濃度」の積に比例するんです!「反応前野登場人物が2つになったので、反応速度はその濃度の積になる」というとこがポイントです。
反応速度が積になるイメージ
それではなぜ、反応速度はAとBの積になるのでしょうか。それは「AとBが衝突するときに反応が起こる」という考え方をとると分かり易いです。
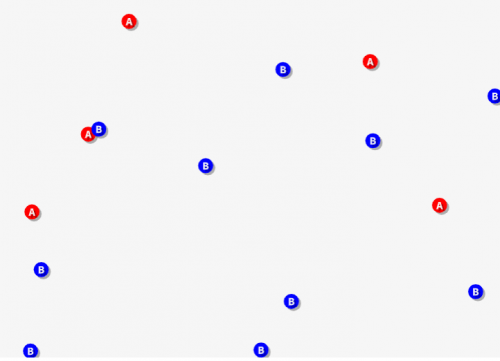
今赤のAの目線で「Bと衝突できる回数」を考えます。このとき、Bの数が少ないのでなかなか衝突することが出来ません。
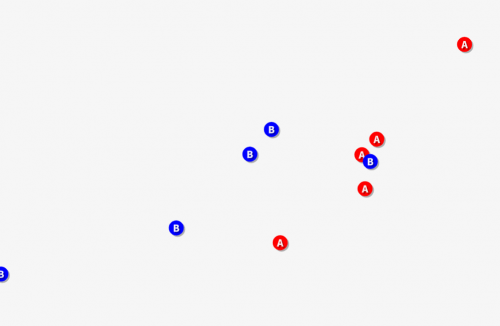
そこでBの濃度を2倍にすると、衝突できる可能性が単純に2倍に増えそうですよね。
また、Aの濃度を2倍にすると、、、衝突する側の機会も2倍に増えそうですよね。
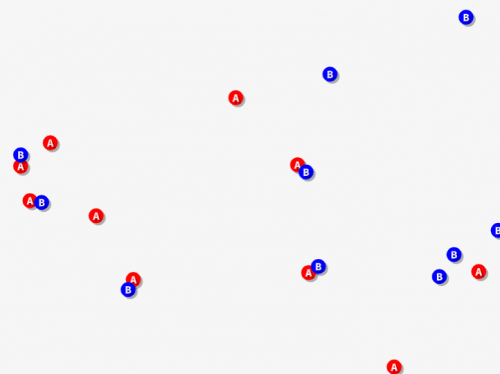
そう考えると2×2=4倍と、積の比例になるんです!
実際はもうちょっと複雑な計算になるはずですが、、、、単純には濃度の積で計算できると考えられるのです!
化学反応速度・化学平衡をシミュレーターを用いて確認しよう!
それでは具体的な化学反応速度・化学平衡をシミュレーターで確認してみましょう!今回は↑で解説してきたように「A + B ⇒ AB 」の化学反応という反応について考えていきます。
- 初期状態の全てAの状態からA + B ⇒ AB の化学反応が進んでいきます(逆反応も同時に進む)
- ↓のスライドバーで、AとBの濃度を調整できます
- ↓の実行ボタンを押すと、反応がはじまります。実際にAとBが衝突して、ABに変化していく様子と、その個数(濃度)の変化グラフをリアルタイムで確認できます
- ABの濃度は、AとBの濃度の積に比例しそうなことを確認しましょう!
* 今回は少数の分子をランダムで動かしてシミュレーションしているため、キレイなグラフにはなりません
シミュレーター結果の考察
シミュレーターでAとBの数を変えると↓のように、片方を2倍にするだけでも紫で示すABのグラフが2倍ぐらいに増えるのがわかると思います。衝突機会はAとBの濃度の積で決まるわけです!
A10個,B10個

A20個,B10個
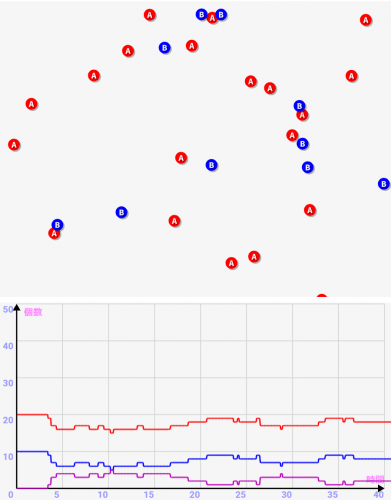
- 化学反応はA + B ⇒ ABという2原子の足し合わせの反応では、その反応速度はAとBの濃度の積に比例する場合が多い
- これはAとBの原子の衝突機会を考えることで示せる
⇒「反応速度」カテゴリ記事一覧
その他関連カテゴリ